Let's learn how to know the length and calulation of vectors in A-Level Maths!
Vector addition
If you imagine that vector a represents a journey [at least, the straight-line distance from the start to the end of the journey] and b another such journey, then a + b is taken to mean:
perform the journey a;
then, from the point where a finishes, perform the journey b;
a + b is then the vector from the start of a to the end of b.
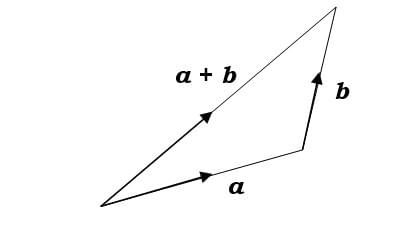
On this diagram, you could also envisage how to add vectors in column notation.
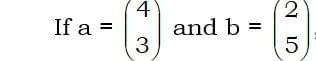
then a + b clearly goes 4 + 2 in the x direction
and 3 + 5 in the y direction. In other words:
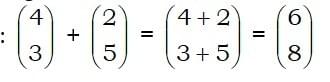
Subtraction
we then define a – b to mean a+ (-b).
Length of a vector
The length [or magnitude] of a vector can be indicated by putting any name of the vector inside modulus signs – a usage which is completely consistent with the arithmetical use of mod signs.
Also, if the vector is shown as AB, then AB will do nicely as its length, just like in ordinary geometry.
And, if the vector is called by a single letter, e.g. a, then its length is usally shown as that same letter but not in bold: a.
Finding that length is just a matter of using Pythagoras.
In the example of
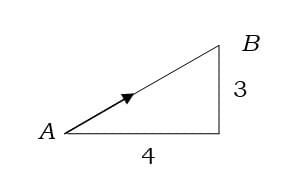
the length of AB is the square root of 42 + 32 which is 5.
In three dimensions, we use an extended Pythagoras.
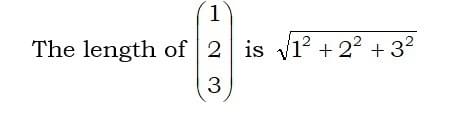
Example
Find the lengths of these vectors:
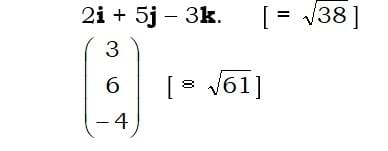
Scalar multiplication
Once vectors are on the scene, we need a name to give to ordinary numbers. That name is ‘scalar’ meaning that ordinary numbers have scale [or size], but no direction.
[Although I would always argue that they do have direction in that positive numbers go one way along a number line and negative numbers go in the opposite direction. So perhaps it would be better tosay that scalars have direction only in one dimension (back and forth along a single straight line) whereas vectors have direction in two or more dimensions.]
We can define scalar multiplication with an example.
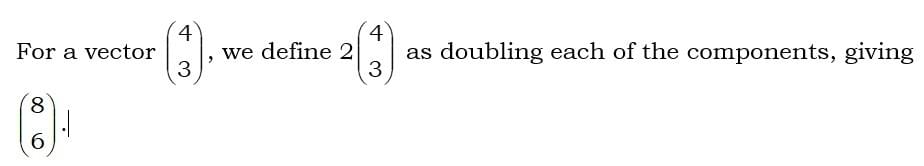
On a diagram, this means preserving the direction of the line representing the vector, but doubling its length.
One special example is what we mean by
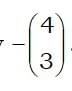
Just like with ordinary algebra, we understand this to mean negative one times the vector which has to mean
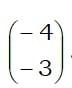
This is a vector which has the same size as the original, but precisely the opposite direction.
Drafted by Eunice (Maths)

