You may or may not have encountered vectors before, but let's learn/review about them from the basics in A-Level Maths!
Vector algebra
They are quantities which have both magnitude anddirection.
Think of them, if you like, as journey vectors, representing a journey as a straight line, direct from itsstart to its finish.
We shall also use position vectors [as the journey from the origin to the given point].
[In M1, we shall use vectors to represent force,acceleration, velocity, momentum …]
We shall develop our use of them, first, in two dimensions and then stretch our results to three dimensions [a stretch that is done very easily with vectors].
Notation
In geometry, AB can denote a line going from A to B or the length of that line [you have to tell from context which it means].
If you intend the line to be seen as a vector, you must clearly indicate the direction in which the line is to traversed.
On a diagram, this is done by adding an arrow to the line. You can also modify the name AB by putting an arrow over the letters:
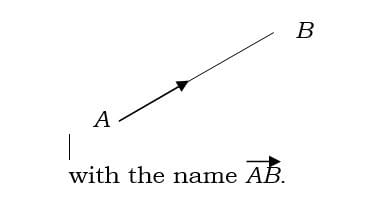
You can also refer to the vector with a single letter name which must be in lower case bold: b.
[Upper case bold letters are reserves for the names of matrices]
In handwriting, you can’t convincingly do bold, so any single letter name for a vector must be underlined instead.
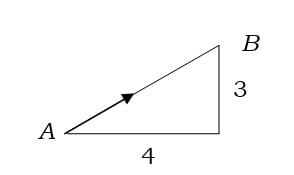
Another way of denoting a vector is with a column of numbers.
The vector shown here, which goes along 4 in the x direction and 3 in the y direction, can be shown as vector
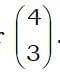
If point A were the origin, then (4, 3) would be the coordinates of point B.
A row like that will always be intended as a coordinate pair and a column intended to be a vector.
Clearly, if A were the origin, then the vector
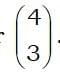
could be used to describe the position of point B. In that case, it’s known as a position vector.
Another notation
We define i and j to be unit vectors [i.e. vectors of length 1] in the directions of the x and y axes.
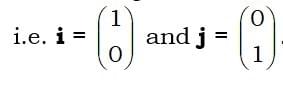
The diagram on page 1 showing the vector

could now be redrawn:
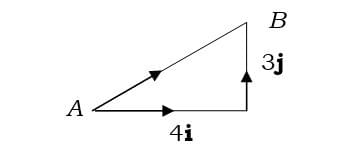
This turns the diagram into a vector addition triangle, giving the original vector as 4i + 3j.
Publishers love this notation because it allows them to put vectors in a single line of print [which is easy and cheap]. In handwriting, it is a lot easier to use the column notation.
If you find a question in i, j notation, you may well want to do it using columns, but it might be as well to move back into i, j for your answer so that your answer is in the same language as the question.
Three dimensions
The move to three dimensions is very easy. Column vectors acquire a third component for the z direction
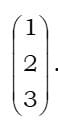
A new unit vector, k, along the z-axis turns i, j notation into i, j, k. Everything else stays the same.
Drafted by Eunice (Maths)

