Let's look into differentiation and the different rules in A-Level Maths!
Chain rule:
The chain rule is used to differentiate composite functions y=f(g(x)) (i.e. functions of a function)
The chain rule operates by making the substitution, u=g(x). Then
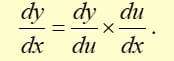
Example: Differentiate
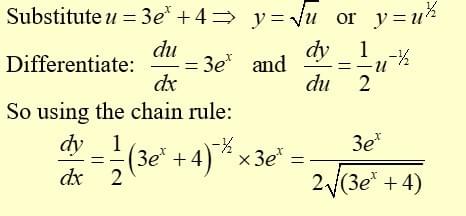
Product rule
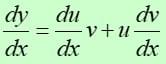
It is used when there is a product of 2 functions.
Example:
Differentiate y= (3x2 - 2x)e1-2x
This is a product of 2 functions:
u = 3x2 - 2x ⇨ du/dx = 6x - 2
v= e1-2x ⇨ dv/dx= - 2e1-2x
Using the productrule formula:
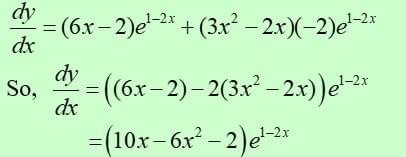
Quotient rule
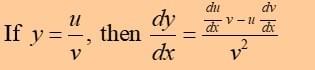
It is used for differentiating quotients (i.e.fractions).
Example: Differentiate
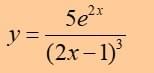

Factorise top in order to simplify:
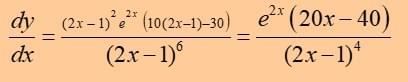
Remember these results:

Finding the derivative when x = f(y):
We use the result
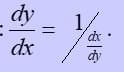
Example:
If x = 4y - y2, find dy/dx in terms of y.

Connected rates of change:
The word rate is associated with differentiation.
Key steps:
(1) Interpret mathematically the information given in the question.
(2) Write down the relevant formula connecting the variables and differentiate it.
(3) Decide on what quantity needs to be calculated.
(4) Use the chain rule to calculate it.
Example:
The volume of a sphere is decreasing at a rate of 20cm3/s. Find the rate at which the radius is increasing when the radius is 3 cm.
Solution:
From question, dV/dt = -20
Connecting formula:
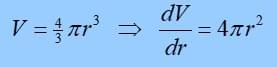
We want dr/dt
using chain rule
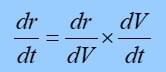
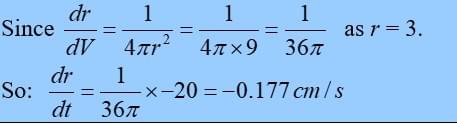
Drafted by Eunice (Maths)

