Let's learn about scaling and covariance in linear regression of A-Level Maths!
Scaling
If one or more variables is scaled using a linear transformation then the new regression equation (in relation to the old one) can be found by substituting the transformation into the original equation.
For example, lets say that a regression line is given by: y = 26.2x - 344
Let’s say the explanatory variable is temperature in Celsius. We want the regression line in terms of Fahrenheit. To do this, we must substitute the formula for Fahrenheit into the original regression equation.
The formula to convert Celsius (x) into Fahrenheit (t) can be found by the below equation:
t = 9/5 x + 32
We need to rearrange this in terms of x.
x = (t - 32) 5/9
Substituting this into the regression line of y = 26.2x - 344 gives:
y =14.6t - 809.8
This formula is now in terms of Fahrenheit. This formula can still be used for extrapolation and interpolation.
Covariance
Covariance measures the extent to which the values of x and y are associated, high with high and low with low. It is given by the formula:
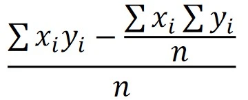
Covariance is denoted by the expression:

When a set of data follows a generally positive gradient, the covariance is positive. The two variables are said to be positively correlated.
When a set of data follows a generally negative gradient, the covariance is negative. The two variables are said to be negatively correlated.
When a set of data follows no clear gradient, the covariance tends to be around 0. It is said that there is no correlation.

Drafted by Eunice (Maths)
Reference
https://www.statisticshowto.com/probability-and-statistics/statistics-definitions/covariance/

