AS/A-Level Mathematics - Correlation

Let's learn about correlation in A-Level Maths!

Correlation 

Correlation can be measured with the product moment correlation coefficient, given by the below expression:

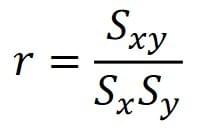
Which means the covariance of the data divided by the (standard deviation of the explanatory variable multiplied by the standard deviation of the response variable). 

The product moment correlation coefficient is denoted by r, which is always within the below range: 

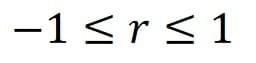
Where -1 indicates perfect negative correlation, 1 indicates perfect positive correlation, and 0 indicates no 

correlation. The product moment correlation coefficient is calculated with the below formula: 

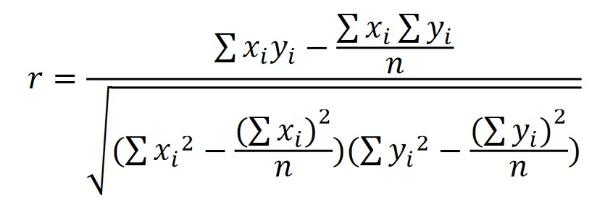
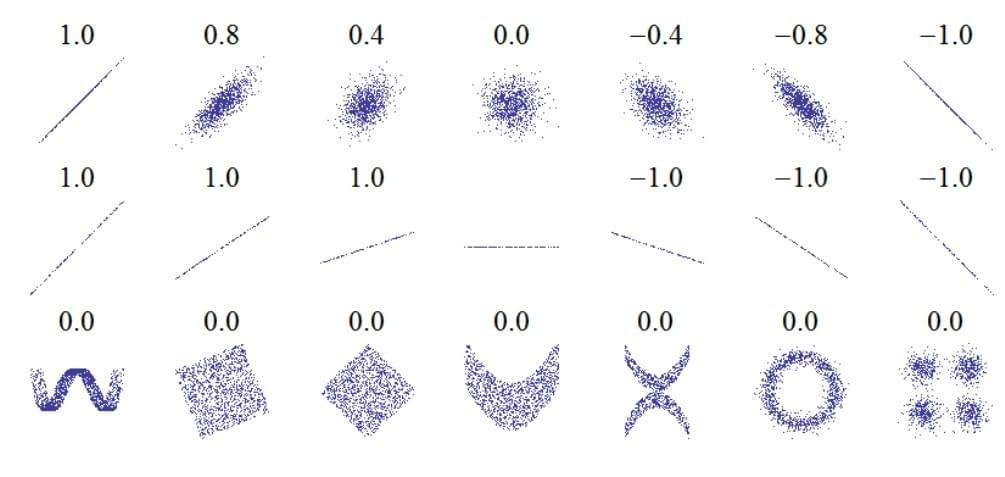
The diagram below shows the value of the p.m.c.c for varying data sets

Correlation Example Question 

A family records for a number of days the midday temperature outside in degrees C, and the number of units of electricity they use in that one day.   

From this Bivariate data, the following values were calculated: 

Σ x_iy_i = 4468.5

Σ x_i = 110.9

Σ y_i = 415

Σ x_i² = 1324.57

Σ y_i² = 17501

n =10

Calculate the product moment correlation coefficient of this data, and make a conclusion about what the p.m.c.c informs us in the context of the question.

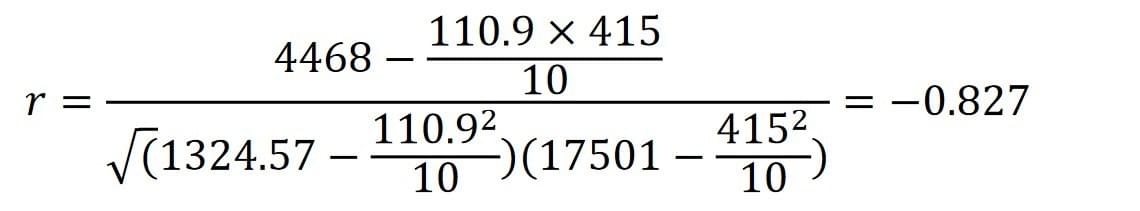
Because the product moment correlation coefficient is negative, one could interpret that the data follows a generally strong negative correlation, so on warmer days, the family uses less electricity.

Scaling 

Scaling, of any kind, like adding values to the data or multiplying them by a constant, does not affect the product moment correlation coefficient at all, because the points are still relative to each other.

Interpreting correlation 

A relationship between two variables may not follow a linear relationship, but may still give a product moment correlation coefficient which is not 0. 

For example, a quadratic relationship may give a p.m.c.c of   -0.1 or 0.1, which would imply extremely slight negative or positive correlation respectively, even though it is clearly not a linear relationship.  

Spurious correlation 

is where the explanatory variable may not be the only cause of the effect on the response variable. This is a common misuse of correlation, where it is assumed that a strong correlation means that the explanatory variable is a direct ‘cause’ of the response variable, and this may not be the case. A third variable may be the cause of the effect on the response variable.

CLICK HERE TO LEARN MORE ABOUT OUR A-LEVEL MATHS COURSES

Drafted by Eunice (Maths)