Let's look at examples of bivariate data to learn more about this topic in A-Level Maths!
So, let’s calculate the least squares regression line for the following Bivariate data:

Important Note: The above sum is calculated by multiplying the data pairs, so (5 X 40)+(10 X 44) etc.
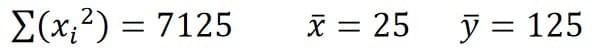
b = (33895 - 9 x 25 x 125) / (7125 - 9 x 252)
= 3.85
So the gradient is 3.85.
a= 125 - 3.85 x 25
=28.83
So the least squares regression line for the above Bivariate data is:
y = 3.85x + 28.83
So what is the significance of this equation for the least squares regression line?
The straight line shown on the diagram below is the plotted version of the equation: y = 3.85x + 28.83
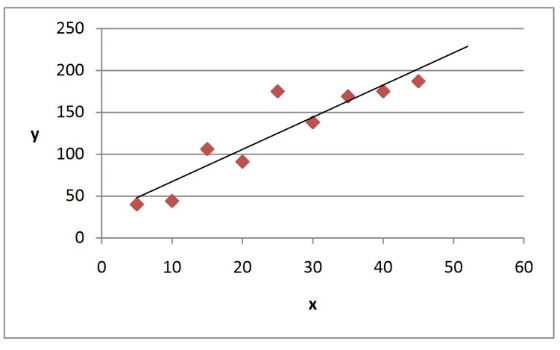
Fitting a straight line to a set of Bivariate data is called fitting a linear regression model. We can use the least squares regression line to predict values of x which are outside the range of the original data.
For example, using the data shown to the left, if we want to predict the value of y which will be given by the value of x=50, we can substitute x=50 into the least squares regression line.
y = 3.85 x 50 + 28.83 = 221.33
Predicting in these cases is called extrapolation. Values predicted by extrapolation must be treated with caution, by analysing the data so as to see whether predicting a value for x will have any implications, and whether or not it’s actually plausible!
Predicting values within the range of the given data is called interpolation. For both interpolation and extrapolation, if a linear line is an appropriate model for Bivariate data, then predicting values of y by substituting unknown values of x is usually reliable.
Linear Regression Example Question
A y on x regression equation is to be calculated for two variables x and y. Given that:
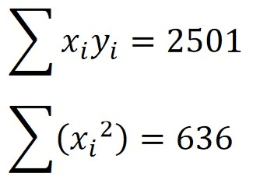
X̅ = 32/9
ȳ = 289/9
Calculate the least squares regression line:
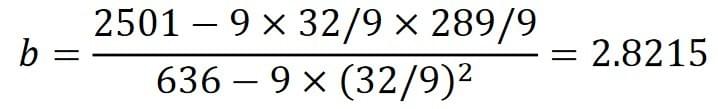
a = 289/9 - 2.8215 x 32/9
= 22.08
So the least squares regression line is given by:
y = 2.8215x + 22.08
Drafted by Eunice (Maths)

