·
The Properties of the Reciprocal Functions
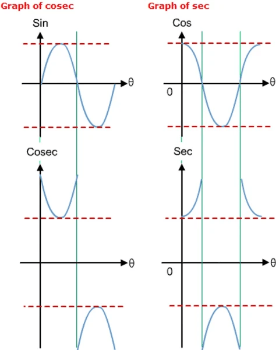
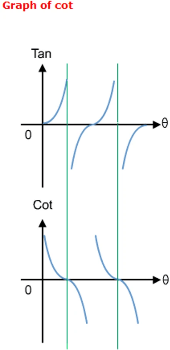
1. The reciprocal of zero is +∞.
2. The reciprocal of +∞ is zero.
3. The reciprocal of 1 is 1.
4. The reciprocal of -1 is -1.
5. Where the function has a maximum value, its reciprocal has a minimum value.
6. If a function increases, the reciprocal decreases.
7. A function and its reciprocal have the same sign.
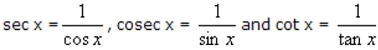
The graphs of sec x, cosec x, cot x
- From a right angled triangle we know that:
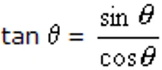
- cos2θ + sin2θ = 1
- It can also be shown that: 1 + tan2θ = sec2θ and cot2θ + 1 = cosec2θ
When it comes to A2/A-level Maths, do you remember the formula of trigonometry?
Formulae for sin (A + B), cos (A + B), tan (A + B)
- Trigonometric functions of angles like A + B and A − B can be expressed in terms of the trigonometric functions of A and B.
- These are called compound angle identities:
- sin (A + B) = sin A cos B + cos A sin B
- sin (A - B) = sin A cos B - cos A sin B
- cos (A + B) = cos A cos B - sin A sin B
- cos (A - B) = cos A cos B + sin A sin B

Double Angle Formulae
- The compound angle formulae can also be used with two equal angles i.e. A = B.
- If we replace B with A in the compound angle formulae for (A + B), we have:
sin 2A = 2(sin A cos A)
cos 2A = cos2A - sin2A
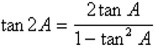
- cos 2A = cos 2A - sin 2A = 1 - 2sin2A = 2cos2A - 1
- The use for this final rearrangement is when integrating cos2x or sin2x.
- We use cos2 x = ½cos 2x + ½ and sin2 x = ½ - ½ cos 2x which we can integrate.
Half Angle Formulae
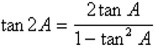
- Using this double angle formula for tan 2A and the two identities:

- We can replace 2A with x and use T for tan(x/2).
- This gives us the following identities, which allow all the trigonometric functions of any angle to be expressed in terms of T.
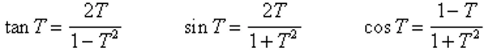
Factor Formulae
- The formulae we have met so far involve manipulating single expressions of sin x and cos x.
- If we wish to add sin or cos expressions together we need to use the factor formulae, which are derived from the compound angle rules we met earlier.
- The compound angle formulae can be combined to give:
2sin A cos B = sin (A + B) + sin (A − B)
2cos A sin B = sin (A + B) - sin (A − B)
2cos A cos B = cos (A + B) + cos (A − B)
−2sin A sin B = cos (A + B) - cos (A − B) - If we simplify the right hand side of each of these equations by substituting A + B = J and A − B = K, we create the factor formulae:
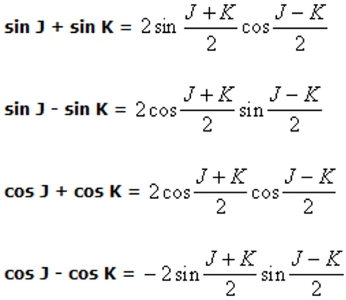
That's the end of the topic!

Drafted by Bonnie (Mathematics)

