AS/A-Level Mathematics - Limits to infinity

Infinity is a very special idea. We know we can't reach it, but we can still try to work out the value of functions that have infinity in them in A-Level Maths.

In previous post, we have seen that 1/∞ = 0

What is the limit of this function as x approaches infinity? 

y = 2x 

Obviously as "x" gets larger, so does "2x".

So as "x" approaches infinity, then "2x" also approaches infinity. We write this:

Infinity and Degree

😎Functions like 1/x approach 0 as x approaches infinity. This is also true for 1/x² etc

😎A function such as x will approach infinity, as well as 2x, or x/9 and so on. Likewise functions with x² or x³ etc will also approach infinity.

😎But be careful, a function like "−x" will approach "−infinity", so we have to look at the signs of x.

Example: 

2x²−5x  

• 2x² will head towards +infinity 
• −5x will head towards -infinity 
• But x² grows more rapidly than x, so 2x²−5x will head towards +infinity  

Compare the Degree of P(x) to the Degree of Q(x):

In a rational function, i.e.:

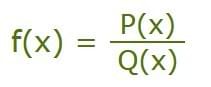
If the Degree of P is less than the Degree of Q ... 

... the limit is 0. 

If the Degree of P and Q are the same ... 

... divide the coefficients of the terms with the largest exponent, like this:  

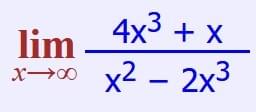
If the Degree of P is greater than the Degree of Q ...

... then the limit is positive infinity ...

... or maybe negative infinity. We need to look at the signs!

We can work out the sign (positive or negative) by looking at the signs of the terms with the largest exponent, just like how we found the coefficients above:

using the example above

• 4x³ (the term with the largest exponent in the top) and 
• -2x³ (the term with the largest exponent in the bottom) 
• 4/-2 is negative. Hence this is heading for negative infinity

Working Out "e"

This formula gets closer to the value of e (Euler's number) as n increases:

(1 + 1/n)ⁿ

At infinity^: (1 + 1/∞ )^∞ = ???

So instead of trying to work it out for infinity (because we can't get a sensible answer), let's try larger and larger values of n:

Yes, it is heading towards the value 2.71828... which is e (Euler's Number) 

So again we have an odd situation:  

• We don't know what the value is when n=infinity 
• But we can see that it settles towards 2.71828... 

so...lim n→∞ : (1 + 1/n)ⁿ = e

CLICK HERE TO LEARN MORE ABOUT OUR A-LEVEL MATHS COURSES

Drafted by Eunice (Maths)

Reference

https://www.mathsisfun.com/calculus/limits-infinity.html