Let's learn how to find the value with limits in A-Level Maths!
There are many ways to get an accurate answer. Let's look at some:
Just Put The Value In
The first thing to try is just putting the value of the limit in, and see if it works (in other words substitution).
Example:
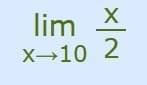
10/2 =5
Factors
We can try factoring.
Example:

If we simply subsitute x=1 into this, we will get 0/0 which is undefined.
By factoring (x2−1) into (x−1)(x+1) we get:
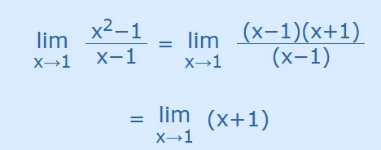
Now we can just substitiute x=1 to get the limit:
1+1 = 2
Conjugate
For some fractions multiplying top and bottom by a conjugate can help.
The conjugate is where we change the sign in the middle of 2 terms like this:

Here is an example where it will help us find a limit:

Evaluating this at x=4 gives 0/0, which is not a good answer!
So, let's try some rearranging:
Multiply top and bottom by the conjugate of the top:
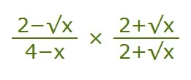
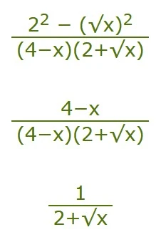
Cancel (4−x) from top and bottom:
So, now we have:
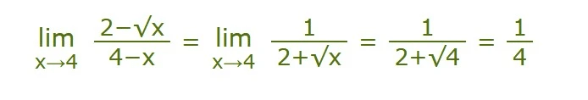
Infinite Limits and Rational Functions
A Rational Function is one that is the ratio of two polynomials
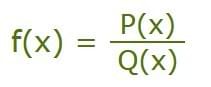
For example, here P(x) = x3 + 2x − 1, and Q(x) = 6x2:
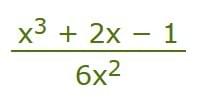
By finding the overall Degree of the Function we can find out whether the function's limit is 0, Infinity, -Infinity, or easily calculated from the coefficients.
Learn about the limits to infinity here.
Drafted by Eunice (Maths)
Reference
https://www.mathsisfun.com/calculus/limits-evaluating.html

