Let's learn about limit in A-Level Maths, which tell us how things turn out when a function reaches a certain value or towards infinity.
Approaching...
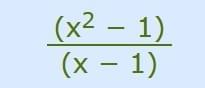
if x=1, it becomes 0 divided by 0.
So instead of trying to work it out for x=1 let's try approaching it closer and closer:
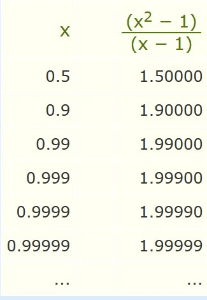
Now we see that as x gets close to 1, then (x2−1) /(x−1) gets close to 2
We want to give the answer "2" but can't, so instead mathematicians say exactly what is going on by using the special word "limit".
The limit of (x2−1) /(x−1) as x approaches 1 is 2
And it is written in symbols as:
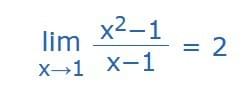
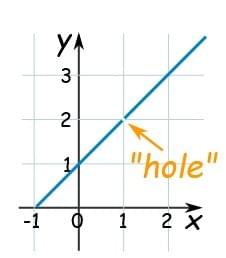
As a graph it looks lik the above:
So, in truth, we cannot say what the value at x=1 is. But we can say that as we approach 1, the limit is 2.
Different from different sides
How about a function f(x) with a "break" - The limit does not exist at "a"
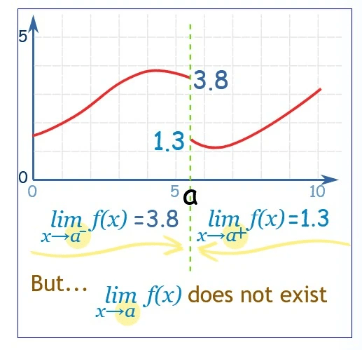
We can't say what the value at "a" is, because there are two competing answers:
- 3.8 from the left, and
- 1.3 from the right
But we can use the special "−" or "+" signs (as shown) to define one sided limits:
- the left-hand limit (−) is 3.8
- the right-hand limit (+) is 1.3
And the ordinary limit "does not exist"
Approaching Infinity
What is the value of 1/∞ ?
We Don't Know!
Maybe we could say that 1/∞ = 0, ... but that is a problem too, because if we divide 1 into infinite pieces and they end up 0 each, what happened to the 1?
In fact 1/∞ is known to be undefined.
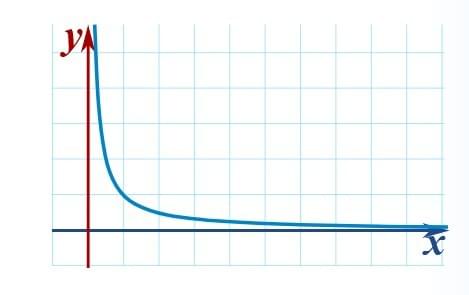
we can see that as x gets larger, 1 /x tends towards 0
We are now faced with an interesting situation:
- We can't say what happens when x gets to infinity
- But we can see that
1/ x is going towards 0
We want to give the answer "0" but can't, so instead mathematicians say exactly what is going on by using the special word "limit".
The limit of 1/ x as x approaches Infinity is 0

Drafted by Eunice (Maths)
Reference
https://www.mathsisfun.com/calculus/limits.html

