Gravitational Force
Gravitational force is an attractive force between two masses. We are pulled towards the ground because the Earth exerts gravitational force to us.
The gravitational force that Earth exerts on us is called the weight.
w = mg
w = weight (N)
m = mass (kg)
g = gravitational field strength (N/kg)
On Earth, g = 10 N/kg
g can differ on different places.
Mass and Weight
Mass does not change for an object wherever the object is. However, the weight of an object can be different on different places.
For example, a person with a mass of 60 kg will weigh 60 x 10 = 600 N on Earth. When this person moves to the moon, which has gravitational field strength that is approximately 1/6 of that on Earth, the mass will still be 60 kg, but the weight will now become 60 x 10/6 = 100 N.
Orbits in the Universe
Gravitational force enables different bodies in the universe to orbit around other bodies.
- Moons orbit around planets. The orbit is almost circular, and the orbital speed is mostly constant in any position of the orbit.
- Planets orbit around the sun. The orbit is almost circular, and the orbital speed is mostly constant in any position of the orbit.
- Comets orbit around the sun. The orbit is highly elliptical, and the orbital speed is higher when they are closer to the sun and lower when they are further away from the sun.
Equation for calculating orbital speed:
v = 2πr / T
v = orbital speed
r = orbital radius
T = orbital period
Example 1
The Earth orbits the Sun once in 365 days. The radius of the Earth's orbit is 150,000,000 km. Calculate the orbital speed of the Earth in kilometers per hour.
Solution.
v = 2πr / T = 2 x π x 150,000,000 km / 365 days = 2 x π x 150,000,000 km / 365 x 24 hours = 110,000 km/h
Example 2
The diagram shows the path followed by a comet as it moves around the sun. A, B, C, D and E are points on the comet's orbit.
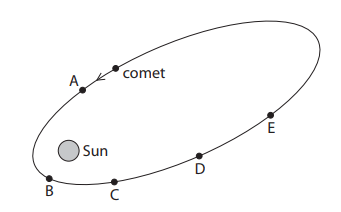
(i) State the name of the force that causes the comet to orbit the sun.
(ii) At which of the points shown is the force on the comet greatest?
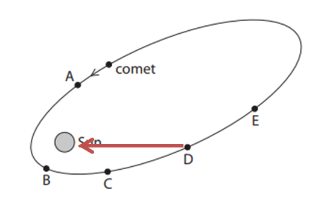
(iii) Draw an arrow at point D to show the direction of the force acting on the comet.
(iv) At which of the points shown does the comet have the greatest kinetic energy?
Solution.
(i) gravitational force
(ii) The gravitational force on the comet is greatest at point B because the comet is closest to the sun at this point.
(iii) The gravitational force should always be directed towards the center of the sun.
(iv) The comet is closest to the sun at point B and therefore has the largest speed at point B. Since KE = 1/2 x mv2, the kinetic energy is greatest at point B where the comet has the largest speed.
Example 3
Deimos is a moon that orbits the planet Mars. Enceladus is a moon that orbits the planet Saturn. Enceladus has a similar orbital period to that of Deimos, but its orbital speed is about 10 times larger. Explain how this is possible.
Solution.
Rearranging the equation for orbital velocity gives:
T = 2πr / v
If the orbital speed of Enceladus is 10 times larger, the orbital radius of Enceladus is 10 times larger than that of Deimos for the orbital period to be same for both moons.

