Radians
Angles can be measured in either radians or degrees where 180° = π radians. If you know that 180° = π radians, you can easily convert between the two.
To convert any given angle from the measure of degrees to radians, the value has to be multiplied by π/180.
So 30° converts to radians as follows:
30π /180 = π/6 radians
To convert from radians to degrees, you simply have to multiply the radian value by 180/π.
To convert π/4 radians into degrees:
180/4 = 45°
Sin, Tan and Cos
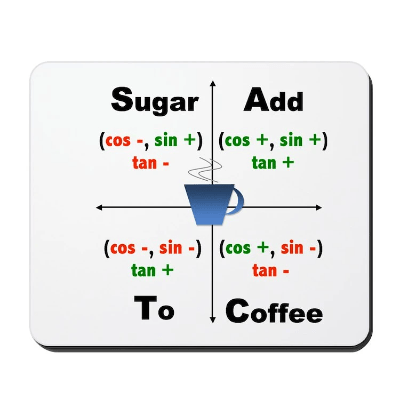
All, Sin, Tan and Cos:
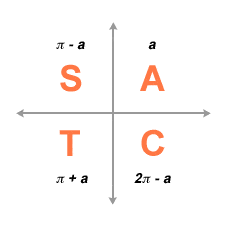
This is an All, Sin, Tan and Cos diagram. This determines whether the outcome of the equation will be positive or negative.
Compound Angle formula:
The compound angle (or addition) formulae are:
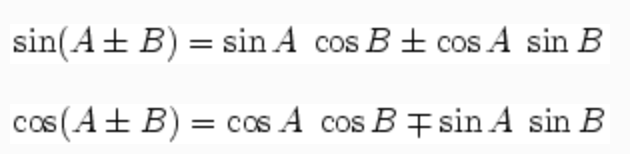
This is commonly seen in a question where you will be asked to give an expansion of Sin or Cos.
You will need to know your exact values to figure these out.
Example:
By writing 75°=45°+30° determine the exact value of sin 75°
sin75°=sin(45+30)°
using the formula for sin(A+B)
= sin45°cos30° + cos45°sin30°
using exact values that you should know
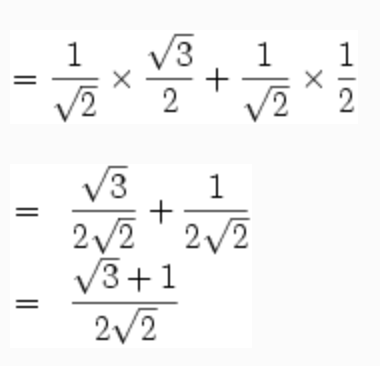
Double Angle Formula:
The double angle formulae are
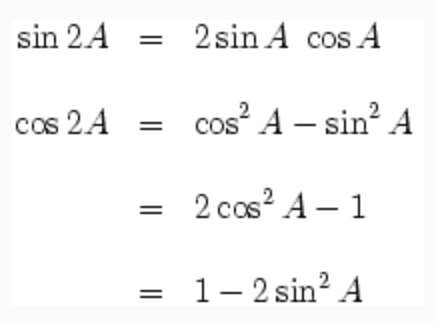
Work hard for your IBDP Mathematics examination!


