IBDP Chemistry - The Nature of Gases

In this topic of IBDP Chemistry, we will be discussing the nature of gases and different gas laws.

The Nature of Gases

In IBDP Chemistry, gases are measured using either mass or volume.

• Their mass can be determined by using the molar mass of the elements involved in the gases.
• For example, for a mole of hydrogen gas (i.e. H₂), the mass of the gas would be the number of hydrogen atoms x the molar mass of a hydrogen atom = 2 x 1.01 = 2.02 g/mol

On the other hand, the volume of gas is determined based on a variety of different factors.

• Pressure, temperature, and the number of moles all play a role in determining the volume of gas.

According to Avogadro's law, regardless of the type of gas, at a given temperature and pressure, the volume of gas occupied by one mole of a gas is the same.

• The molar volume of a gas at standard temperature and pressure (STP, where T = 273K and P = 1.00 x 10⁵ Pa) is 22.7 dm³/mol.
• Avogadro's law is based on several assumptions about gases - it assumes that gases are ideal.
• We will discuss the nature of ideal gases and their difference to real gases in another post, so be sure to keep an eye out for that.

The use of this concept and the molar volume of gases helps simplify our calculations when we are asked to find the volume of a gas formed from a chemical reaction.

For example, say we are asked to find the volume of H₂ gas formed when 0.0500mol of Li is reacted with excess HCl, assuming the reaction was under STP conditions.

• First, as with any question relating to stoichiometric relationships, we have to write out the balanced chemical equation for the reaction.
• The chemical equation for the reaction is as follows: 2Li (s) + 2HCl (aq) → 2LiCl (aq) + H₂ (g)
• Next, we have to determine the number of moles of H₂ gas was formed. We can do this by using the molar ratios given in the chemical equation.
• We know that HCl was in excess (as mentioned in the equation), thus we know that the limiting reagent will be the Lithium.
• From the question, we know we have 0.0500 moles of Li, and the molar ratio of Li to H₂ is 2:1 (for every 2 moles of lithium, one mole of H₂ gas is produced).
• Therefore, we can determine the number of moles of H₂ gas by dividing the moles of Li by 2 - 0.0500/2 = 0.025mol H₂
• Now that we have the moles of H2 produced, we can use the molar volume of gas to find the volume of H₂.
• We can simply multiply the moles of H2 by the molar volume of gas to determine the volume of H2 - 0.025 x 22.7 = 0.5675 dm³

Notes about questions related to gases and calculating the volume of gases:

• In the question above, the limiting reagent of the reaction was already given. However, in some questions, you may be tested on both your knowledge about limiting and excess reagents and the molar volume of gases. Be sure to practice questions related to both areas of knowledge.
• If you are unsure about limiting and excess reagents, click here to learn more.
• Sometimes, you may need to convert the volume of gas into moles - the conversion between moles and volume of gases is shown below.
• To convert from moles to volume, simply multiply the mole of the gas by the molar volume of gas.
• To convert from volume to moles, divide the volume of gas by the molar volume of gas.
• In IBDP Chemistry exams, the molar volume of gas is given in the data booklet. Sometimes the value may be 22.4dm³/mol, sometimes it is 22.7dm³/mol. In your exams, you don't need to memorise the molar volume, simply follow the molar volume written in the data booklet.

Gas Laws

In IBDP Chemistry, the relationship between temperature, pressure and volume of gas (when given a fixed mass of gas) can be described by three gas laws.

• Boyle's Law
• Charles's Law
• Gay-Lussac's Law

Boyle's Law describes the relationship between pressure and volume of gases at a constant temperature.

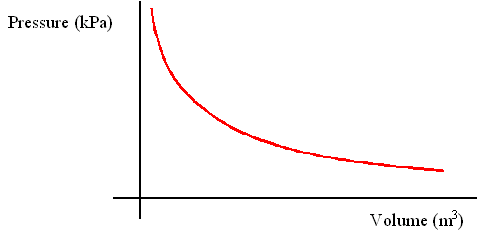
• Boyle discovered that for a fixed mass of gas, the pressure of the gas is inversely proportional to the volume of the gas at constant temperature.
• This makes sense, given that pressures is created when the gaseous molecules hit the surrounding surfaces of the container it is in. The more the molecules collide the surrounding surfaces, the higher the pressure.
• At constant temperature, the gases will be moving at a constant rate. Thus, as the volume decreases, the gases will be in a more confined space, which means they will collide with the walls of the container a lot more, leading to an increase in pressure.
• Boyle's law can be expressed as PV = a constant or P₁V₁ = P₂V₂ (where P₁ = initial pressure, V₁ = initial volume, P₂ = final pressure, V₂ = final volume.)
• This equation can be used to find the volume of a gas after a known change in pressure, if given the intial pressure and volume of gas. It can also be used to find the pressure of a gas after a known change in volume, if given the intial pressure and volume of gas.

Charles's Law describes the relationship between the temperature and volume of gases at a constant pressure.

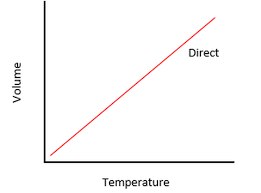
• Charles discovered that for a fixed mass of gas, the temperature of the gas is directly proportional to the volume of gas at constant pressure.
• This makes sense, given that an increase in temperature means that the gas molecues will move at a faster rate.
• At constant pressure, the rate of collision between the walls and gas molecules should be the same, so when the molecules move at a faster rate, to maintain constant pressure, the volume of the container must increase.
• Charles's law can be expressed as V/T = a constant or V₁/T₁ = V₂/T₂ (where T₁ = initial temperature, V₁ = initial volume, T₂ = final temperature, V₂ = final volume.)
• This equation can be used to find the volume of a gas after a known change in temperature, if given the intial temperature and volume of gas. It can also be used to find the temperature of a gas after a known change in volume, if given the intial temperature and volume of gas.

Gay-Lussac's law describes the relationship between the temperature and pressure of gases at a constant volume.

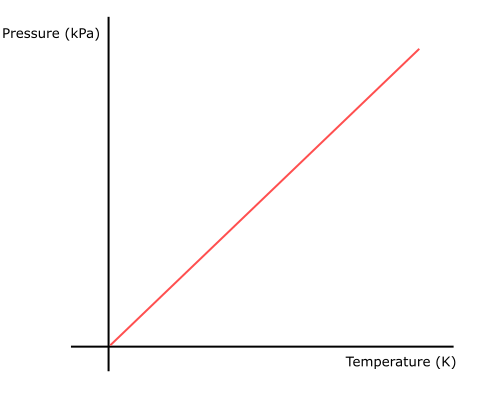
• Gay-Lussac discovered that for a fixed mass of gas, the temperature of the gas is directly proportional to the pressure of gas at constant volume.
• This makes sense, given that at a higher temperature, the gas molecules will move at a faster rate.
• With a constant volume, the increase in rate of movement of gas molecules will increase the rate at which the molecules collide with the walls of the container, which would result in an increase in pressure.
• Gay-Lussac's law can be expressed as P/T = a constant or P₁/T₁ = P₂ /T₂ (where T₁ = initial temperature, P₁ = initial pressure, T₂ = final temperature, P₂ = final pressure.)
• This equation can be used to find the pressure of a gas after a known change in temperature, if given the intial temperature and pressure of gas. It can also be used to find the temperature of a gas after a known change in pressure, if given the intial temperature and pressure of gas.

Combining the equations together, we can get a combined gas laws that connects pressure, temperature and volume into one equation.

• P₁V₁/T₁ = P₂V₂/T₂ (where P₁,V₁ and T₁ are the initial pressure, volume and temperature, and P₂, V₂ and T₂ are the final pressure, volume and temperature).
• When using this equation, ensure that the unit for each variable (i.e. pressure, volume and temperature) are the same for both initial and final values.
• e.g. if T1 is given in Kelvin (K), then T2 should also be given in Kelvin (K)

It is also important to note that these gas laws all assume that the gases behave ideally - the concept of ideal gases will be discussed in future posts.

This is the end of this topic.

Check out with our IB Chemistry Tutor! We are here to help 😀