IBDP Chemistry - Chemical Reactions and Equations

In this topic of IBDP Chemistry, we will be learning about chemical reactions, and how they can be represented by chemical equations.

Chemical Reactions

In IBDP Chemistry, chemical reactions occur between different substances. There are several properties of chemical reactions:

• In each chemical reaction, there are reactants and products.
• Reactants are the substances that are used to produce the chemical reaction - some reactions may also require other conditions to be fulfilled.
• These conditions could include the temperature at which the reaction takes place, whether catalysts are involved etc.
• Products are the substances which are formed from the reaction.
• When a chemical reaction occurs, there is a energy change between the reacting system and the surroundings.
• When a reaction occurs, the bonds in the reactants break, and new bonds are formed to create the products.
• The breaking of bonds in the reactants absorbs energy from the surroundings, whereas the formation of bonds in the products result in a release of energy into the surroundings. These are the energy changes that occur during a chemical reaction.
• There is a fixed relationship between the number of particles of reactants and products - this results in no overall change in mass during the reaction.
• This is known as the stoichiometry of the reaction.

Chemical Equations

In IBDP Chemistry, chemical reactions can be represented by chemical equations. As you progress through chemistry, you will be expected to be able to write and understand chemical equations, and use them to solve problems.

This is the typical structure of a chemical equation:

• Reactants are written on the left side, and products are written on the right side.
• An arrow (pointing towards the right) is used to represent the direction of the chemical reaction (i.e. that the reactants will become the products).
• The single arrow is used when the reaction goes to completion (i.e. all reactants will become products).
• Sometimes, the reaction conditions are written on the arrow.
• If the reaction is reversible (i.e. the reactants can form products, and the products can also become the reactants), then a double arrow is used.

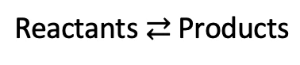
When writing chemical equations, it is often also important to note down the state of each substance - whether they are solid, liquid, gas or in an aqueous solution. These are conveyed through the use of state symbols, as shown below.

It is important to include state symbols in your chemical equations, as the physical states of the reactants can affect the rate of reaction and the overall energy change.

Below is an example of a chemical equation explaning the reaction between calcium carbonate and nitric acid:

Balancing Chemical Equations

In IBDP Chemistry, it is important to ensure that all chemical equations are balanced. What does this mean? It means that the number of each atom has to be the same on both sides.

• For example, if you have 2 oxygen atoms in the reactants, then you must have 2 oxygen atoms in the products.

When balancing equations, we will need to manipulate the coefficients in the chemical equation.

• The coefficients are the numbers in front of each substance involved in the chemical reaction (whether it be a reactant or a product).
• If there is no number in front of the substance, then the coefficient is considered to be '1'.
• The coefficients of the chemical equation give the molar ratio of the reaction - it tells us how many moles of each reactant is needed, and how many moles of each product is formed.
• In the example above (the reaction between calcium carbonate and nitric acid), the coefficients tell us that two moles of nitric acid (HNO₃) reacts with one mole of calcium carbonate (CaCO₃) to product one mole of calcium nitrate (Ca(NO₃)₂), one mole of carbon dioxide (CO₂) and one mole of water (H₂O).
• You can multiply the quantity of each reactant/product by any factor, but the molar ratio between the reactants and products must stay the same.
• e.g. Refering to the reaction above, you can multiply the quantities by two, and react two moles of calcium carbonate with four moles of nitric acid to create two moles of each product - since you have multiplied the quantity of each reactant/product by a factor of 2, the molar ratio still stays the same.

We will now work through an example of balancing a chemical equation. Say we are looking at the combustion of ethane (C₂H₆):

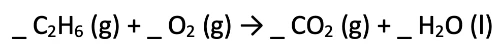
• The first step would be to count the number of each atoms on each side of the equation, assuming that the coefficients of each substance is 1.
• Starting with the reactants side - there are 2 Carbons (C), 6 Hydrogens (H) and 2 Oxygens (O).
• On the products side - there are 3 Oxygens (2 from the carbon dioxide and 1 from water), 2 Hydrogens, and 1 Carbon.
• We can already see that the equation is not balanced - the number of atoms on each side are not the same.
• The next step would be to start manipulating the coefficients.
• We can start by looking at the number of carbon atoms. On the reactants side, there are 2 carbons, but there is only 1 carbon on the products side. Thus, we can change the coefficient of the carbon dioxide to 2, since it is the only compound containing carbon - this would ensure there are 2 carbon atoms on the products side.

• Now, we can count the number of each atoms on each side again.
• Reactants - 2 carbons, 6 hydrogens, 2 oxygens.
• Products - 2 carbons, 2 hydrogens, 5 oxygens.
• We can see the equation is still not balanced - the number of hydrogens and oxygens are still different on both sides.
• We can continue by attempting to balance the hydrogens. Since there are only 2 hydrogens on the products side (from the water), we can change the coefficient of the water molecule to 3.
• This would create 6 hydrogen atoms, since each water molecule has 2 hydrogens, and we have now have 3 water molecules

• Again, we count the number of atoms on each side.
• Reactants - 2 carbons, 6 hydrogens, 2 oxygens.
• Products - 2 carbons, 6 hydrogens, 7 oxygens.
• Now, we only have to balance the oxygens, and we can do this by changing the coefficient of the oxygen molecule on the reactants side.
• Given that each oxygen molecule consists of 2 oxygen atoms, we will need 3.5 oxygen molecules in order to form 7 oxygen atoms.

• However, we want to avoid non-whole number coefficients - we want to ensure that the coefficients gives the simples, whole number molar ratio.
• Thus, we can double all of the coefficients in order to obtain the simplest, whole number coefficients.

• As a final step, we can check to make sure the number of atoms on each side are the same.
• Reactants - 4 carbons, 12 hydrogens, 14 oxygens.
• Products - 4 carbons, 12 hydrogens, 14 oxygens (8 from CO₂, 6 from H₂O)
• The equation is finally balanced.

Tips for balancing equations:

• Only change the coefficients - DO NOT change any of the subscripts.
• CBEThe subscripts show the fixed ratio of atoms in a molecule of each substance - these cannot be changed.
• Only make one change at a time, and check the number of atoms on each side after each change.
• If you get to a point where you just need a fractional amount of a compound, write it in, and then multiply everything by the denominator of the fraction.
• e.g. as seen in the example above, we needed 3.5 (= 7/2) molecules of oxygen, so we multiplied all the coefficients by 2.

Ionic Equations

In IBDP Chemistry, you may sometimes be asked to use ionic equations to write out reactions that involve ionic compunds. This is because ionic compounds are completely dissociated in solutions (i.e. they are separated into their respective ions).

• For example, salt (NaCl) is an ionic compound consisting of Na⁺ and Cl^- ions.
• As a solid, the compound will consist of the ions bonded together, forming NaCl. However, when dissolved in water, the Na⁺ and Cl^- ions separate from each other.

Ionic equations involve writing out the different ions involved in the reaction, including their charge (either positive or negative charge). For example, when a silver nitrate (AgNO₃) solution is added so a sodium chloride (NaCl) solution, a precipitate of silver chloride (AgCl) is formed. The following ionic equation can be written:

Since the NO₃^- and the Na⁺ ions were not involved in the reaction, the ionic equation can be rewritten as:

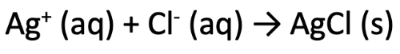
This is the end of this topic.

Check out with our IB Chemistry Tutor! We are here to help 😀