1. Subtending
•In I/GCSE Mathematics, when an angle is created between two lines,
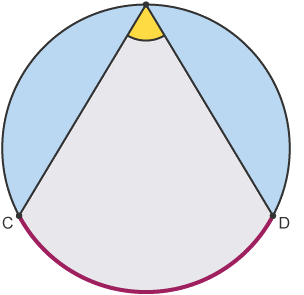
•The angle in between the two lines is subtended between the arc C and D
2. Angles at the Centre and Circumference
•The angle subtended at an arc is twice the size of an angle subtended at the circumference
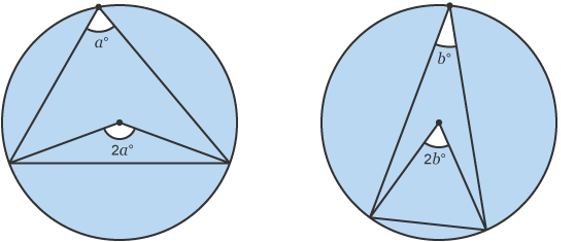
•More simply the angle at the centre is double the angle at the circumference
Proof
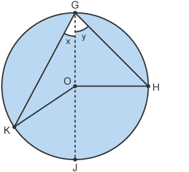
•Let angle OGH = y and angle OGK = x.
• Angle y = angle OHG because GOH is an isosceles.
Lengths OH and OG are both radii.
• Angle x = angle OKG because GOK is an isosceles.
Lengths OK and OG are also radii.
•Angle GOH = 180-2y
Angle GOK = 180- 2x (angles in a triangle add up to 180°)
•Angle JOH = 2y
Angle JOK = 2x (angles on a straight line add up to 180°)
• The angle at the centre KOH (2y+2x) is double the angle at the circumference KGH (x+y).
3. Angles in the Same Segment
•The angle at the circumference subtended by the same arc are equal
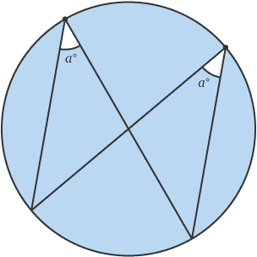
•Simply the angles in the same segment are equal
•Angles a = a
Proof
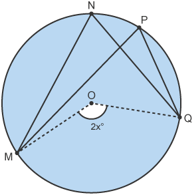
•Let the reflex angle MOQ = 2x
Using the circle theorem the angle at the centre is twice the angle at the circumference.
•Angle MNQ = x and angle MPQ = x
Therefore angle MNQ = angle MPQ.
4. Cyclic Quadrilaterals
•In I/GCSE Mathematics, a cyclic quadrilateral is a quadrilateral drawn inside a circle where every corner of the quadrilateral must touch the circumference.
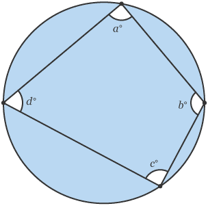
•The opposite angles in a cyclic quadrilateral add up to 180°
•E.g. a + c = 180°
b + d = 180°
Proof
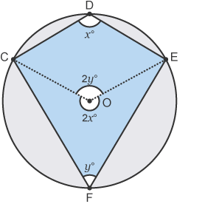
• Let angle CDE = x and angle EFC = y
•!Remember the angle at the centre is double
the angle at the circumference!
•Angle COE = 2y and the reflex angle COE = 2x
•Angles around a point add up to 360°
• 2y + 2x = 360°
• 2y/2 + 2x/2 = 360° /2
• So y and x = 180°

