5. Angles in a Semi-Circle
•The angle at the circumference in a semi-circle is a right angle.
•Angle APB = 90°
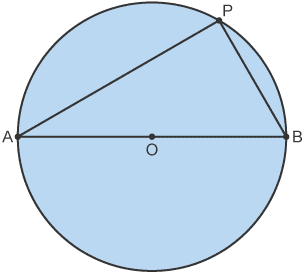
Proof
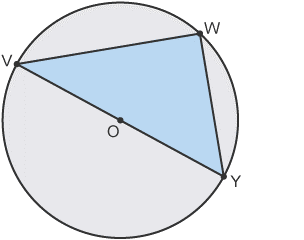
•The angle on a straight line is 180°. So the angle VOY = 180°.
•The angle at the centre is double
the angle at the circumference.
• Angle VWY = 1/2 Angle VOY
• 1/2 x 180° = 90°
•Angle VWY = 90°
6. Tangents
•The angle between a tangent and a radius is 90°
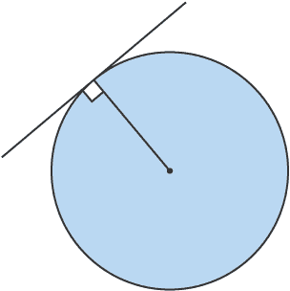
Proof

• The angle between the tangent is 90°
• Angle BCO = Angle BAO = 90 °
• AO and OC are both radii of the circle.
• Length AO = Length OC
7. Tangents
•Tangents which meet at the same point are equal in length
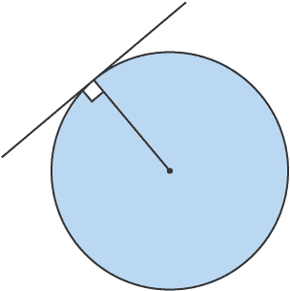
Proof
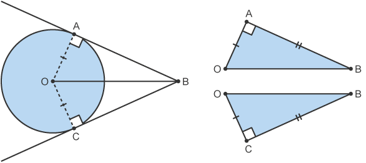
•If you draw the line OB it creates two triangles OCB and OAB they share the length OB, the triangles are congruent because of the SAS rule
•Two of the sides are the same length: OB = OB and OC = OA
•One of the angles is equal in size: OCB = OAB
•Congruent triangles are identical.
•So length CB = AB.
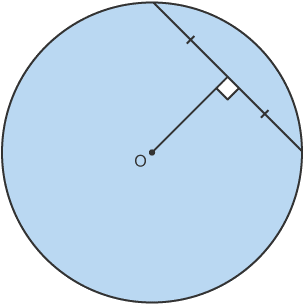
8. Chords
•The perpendicular from the centre of a circle to a chord bisects the chord.
* A straight line joining two points on a circle is a chord.
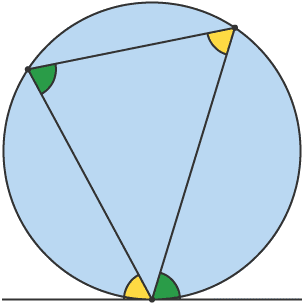
9. Alternate Segment
•The angle between a tangent and a chord is equal to the angle in the alternate segment.
Proof
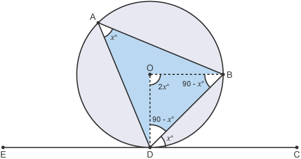
• Let Angle CDB = x
The angle between a tangent and the radius is 90°
• Angle BDO = 90 – x
• Triangle DOB is isosceles so:
• Angle DBO = Angle BDO = 90 – x
• Angles in a triangle at up to 180° so:
• Angle DOB = 180 – DBO – BDO
Angle DOB = 180 – (90 – x) – (90 – x) = 2x
•The angle at the centre is double the angle at the circumference
• Angle DAB = x therefore BDC = DAB
You finish reading all circle theorems in I/GCSE Mathematics.
Well done!


