Inverse Proportion
if two quantities are related in such a manner that if one quantity increases by a factor k and the other decreases by a factor of 1/k then the quantities are said to be inversely proportional.
In the case of hiring the van we say that
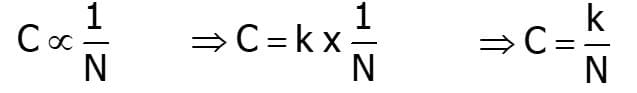
The product C x N is constant and the points lay on a curve of the form y = 1/x

Example 1:
Boyle’s Law states that at constant temperature, the volume V of a gas is inversely proportional to its pressure P. When the pressure is 600 N/m2 the volume is 4m3. Find:
(a) The volume when the pressure is 400 N/m2
(b) The pressure when the volume of the gas is 5 m3
Remember: Strategy for solving proportion problems
1. Find the value of k (the constant of proportionality).
2. Use k together with given values to answer the question.

Example 2:
The cost C of hiring a transit van is inversely proportional to the number of people N, hiring it. If Robert hires the van himself, the cost will be £120. Find:
(a) The cost per person if a party of 4 people hire the van.
(b) The number of people hiring the van if the cost per person is £7.50.
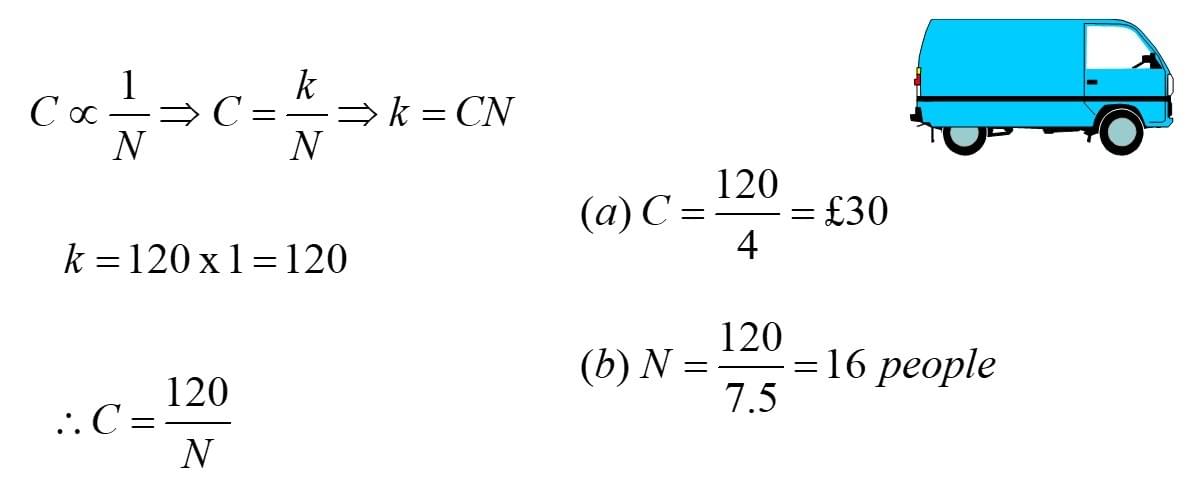
Example 3:
The air pressure P that is delivered by a bicycle pump is inversely proportional to the square of its diameter D. If 8 units of pressure is delivered by a 20 mm diameter pump, find:
(a) The pressure delivered by an 18 mm pump.
(b) The diameter of a pump delivering 6 units of pressure.

Your turn now!!
The force of attraction F, between two magnets is inversely proportional to the square of their distance apart D. When the magnets are 2 cm apart the force of attraction is 24 units. Find:
(a) The force of attraction between two magnets that are 1/2 cm apart.
(b) The distance between two magnets when the force of attraction is 6 units.
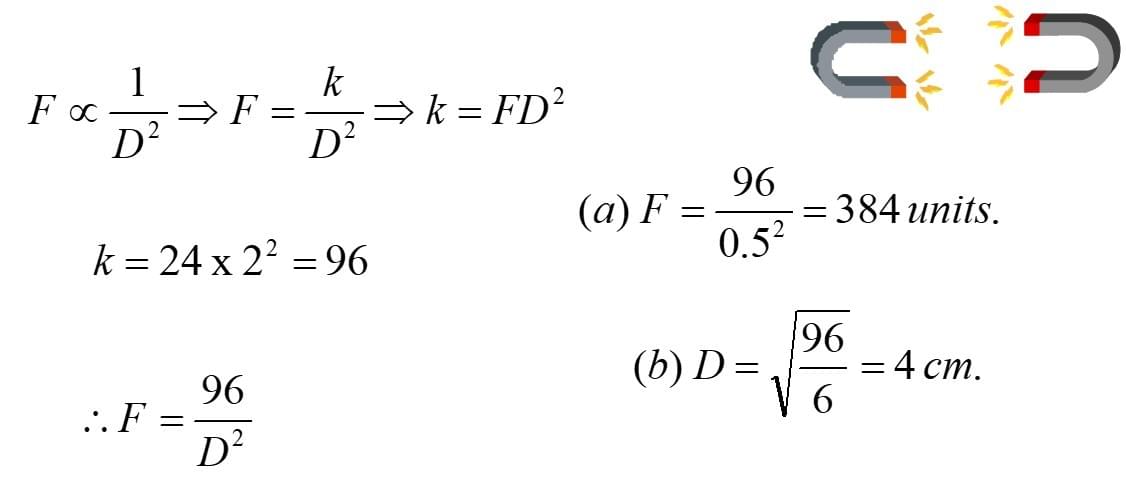
That's all for this session in I/GCSE Mathematics.


