L'Hôpital's Rule can help us calculate a limit that may otherwise be hard or impossible. Let's learn about this in A-Level Maths.
It says that the limit when we divide one function by another is the same after we take the derivative of each function (with some special conditions shown later).
In symbols we can write:
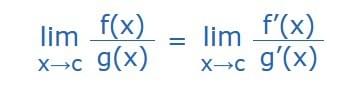
The limit as x approaches c of "f-of−x over g-of−x" equals the the limit as x approaches c of "f-dash-of−x over g-dash-of−x"
the ’ on each function means to take the derivative.
Example:
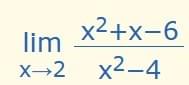
if x=2, it will become 0/0
Now try L'Hôpital!
Differentiate both top and bottom:
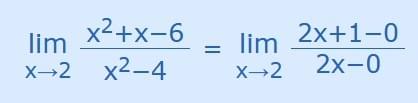
Now we just substitute x=2 to get our answer:

Here is the graph, notice the "hole" at x=2:
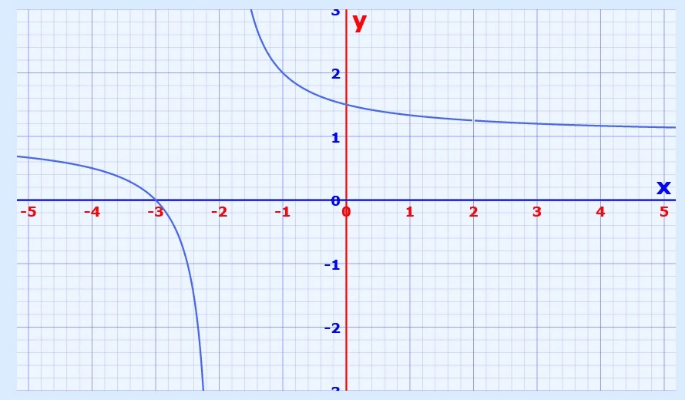
Note: we can also get this answer by factoring, see here.
Conditions
Differentiable
For a limit approaching c, the original functions must be differentiable either side of c, but not necessarily at c.
Likewise g’(x) is not equal to zero either side of c.
The Limit Must Exist
This limit must exist as:
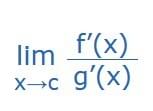
example:
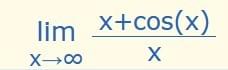
differentiating top and bottom, we get:
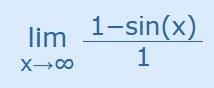
And because it just wiggles up and down it never approaches any value.
So that new limit does not exist!
And so L'Hôpital's Rule is not usable in this case.
BUT we can do this:
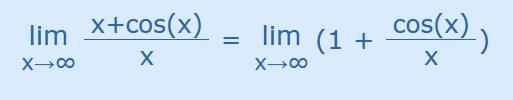
As x goes to infinity then cos(x)/x tends to between −1/∞ and +1/∞, and both tend to zero.
And we are left with just the "1", so:
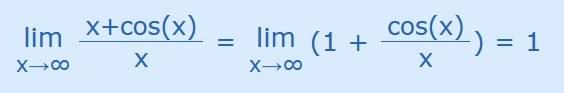
Drafted by Eunice (Maths)
Reference
https://www.mathsisfun.com/calculus/l-hopitals-rule.html

