I/GCSE Mathematics Question Analysis Topic: Mathematics - Short Questions
Exam Questions:
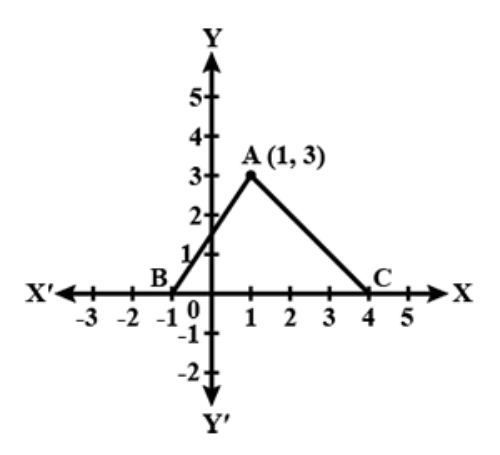
1) Find the area of triangle ABC (in sq. units).
2) If k, 2k−1 and 2k+1 are three consecutive terms of an A.P., what is the value of k?
Answers:
For I/GCSE Mathematics, you should know:
1) We're given that the coordinates of points A, B and C are A(1,3), B(-1, 0) and C(4, 0).
Next, let's draw a downward line from point A to the X-axis, which lands on (1, 0) (which we will call point D).
In triangle ADC, AD = 3 units and DC = 3 units.
The area of triangle ADC is 1 / 2 x DC x AD
= 1 / 2 x 3 x 3 = 9 / 2 cm2.
In triangle ADB, AD = 3 units and DB = 2 units.
The area of triangle ADB = 1 / 2 x DB x AD
= 1 / 2 x 2 x 3 = 3 cm2
So, adding these two together:
Area of triangle ABC = area of triangle ADC + area of triangle ABD
= 9 / 2 + 3 = 15 / 2 = 7.5 cm2
2) The three consecutive terms k, 2k - 1 and 2k + 1 are an arithmetic progression (A.P.).
From this, we can understand that the second term - first term is equivalent to the third term - second term.
i.e.
2k - 1 - k = 2k + 1 - 2k + 1
k - 1 = 2
k = 3
Work hard for your I/GCSE Mathematics examination!
End of analysis. Great!


