·
Linear Graphs
- y = mx + c
- m = Gradient = change in y ÷ change in x
- = up ÷ across
- To calculate the gradient, find 2 points along the line, then work out change in y and change in x
- E.g. (3,3) and (7,5)
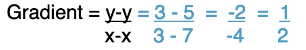
- c = y axis intercept
- To work out the value of C in order to plot the graph, work out the gradient, then substitute known x and y values as well as the gradient to find out c.
- E.g. Given = (0,1), (1,3)
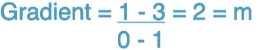
- y = 2x + c
→ 3 = 2(1) + c
→ 3 = 2 + c
→ c = 1
→ y = 2x + 1 - When x = 0, y always = c
- E.g. given (0,5), c = 5
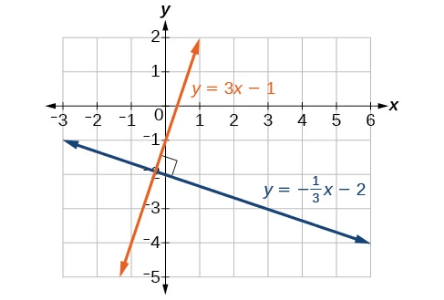
Perpendicular Lines
- Negative reciprocals of each other
- E.g. y = 3x + 4 and y = -⅓x +6
- Intercept value does not matter
- If lines are perpendicular, when you multiply the gradients, they should = -1
- m1 x m2 = -1
- e.g. 3 x -⅓ = -1
Parallel Lines
- Parallel lines have the same gradient value, so y = 2x + 5 is parallel to y = 2x -7.
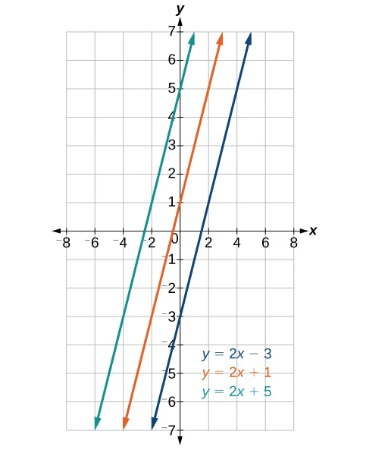
Solving simultaneous equations graphically
- Plot both equations on graph - using chosen method e.g. elimination/substitution
- Where they intersect, the co-ordinate is the y and x values of the simultaneous equation
- E.g. (6,7)
- x = 6, y = 7
- Max Speed = Greatest ÷ Shortest
That's the end of the topic!

Drafted by Bonnie (Mathematics)

