·
Probability
= (number of ways) / (total number of possible outcomes)
= (Frequency of desired outcomes) / (no.of trials)
For example, tossing a die
- P(6) - probability of getting a six = 1/6 —> chance/total possible results
- Probabilities add to 100%
- Probabilities add to 1, e.g. P(0.3) +P(0.7)
Venn Diagrams
- U = or ⟶ both options, e.g. A U B’— A or not B
- ∩ = and/but also ⟶ Same time e.g. A ∩ B — A but also B
Mutually exclusive
- Not at the same time (cannot happen) - e.g. picking a letter that is S and a vowel - P(A and B)
Mutually exhaustive
- One or more can occur e.g. P(A and B) — P(heart and king)
Exhaustive event
- When all possible outcomes have been used up, only probability is 1
Independent event
- Does not affect the next event e.g. roll dice twice
Dependent event
- Affected by another event
Expectation
- Long-run average you would get if a test was repeated many times.
- Expectation = nP (no. trials x probability)
- E.g. Probability of heads with biased coin = 3/4
- Coin thrown 200 times
- Expectation = nP = 3/4 x 200 = 150
When it comes to IGCSE/GCSE Maths, do you remember the following rules?
Rules
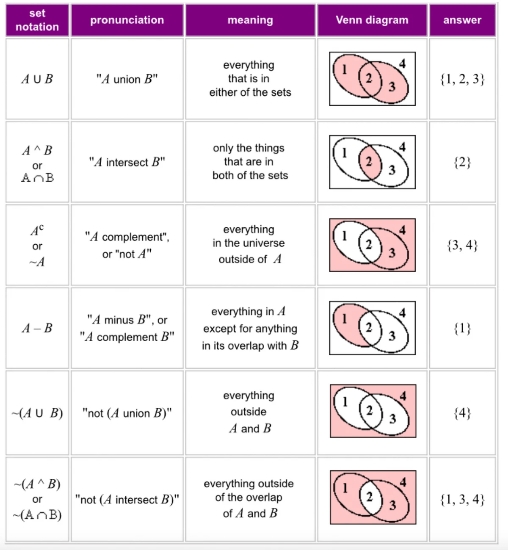
- A U B = A union B = A or B
- A ∩ B = A and B = A intersect B
- A’ = Complement A = everything that does not include A
- ∅ = empty set
- ∈ = an element of A/B e.g. 1 in A
- ∉ = Not an element
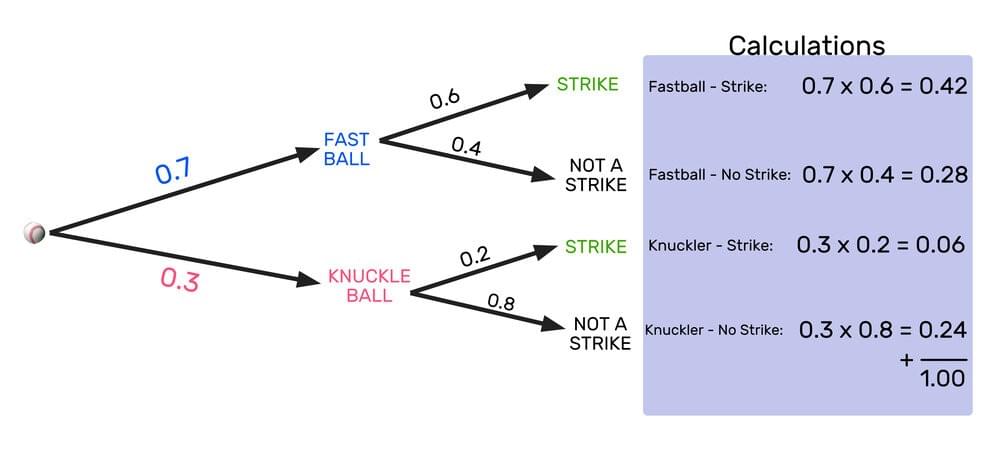
Tree diagrams
- Multiply across branches to find combined probability of 2+ events.
References:
1. https://www.mashupmath.com/blog/probability-tree-diagrams
That's the end of the topic!

Drafted by Bonnie (Mathematics)

