·
Circle Theorems
1. Angles Subtended on the Same Arc
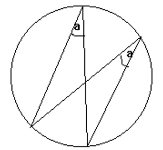
- Angles formed from two points on the circumference are equal to other angles, in the same arc, formed from those two points.
2. Angle in a Semi-Circle
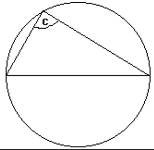
- Angles formed by drawing lines from the ends of the diameter of a circle to its circumference form a right angle.
- c is a right angle.
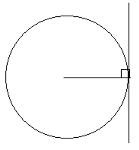
3. Tangents
- A tangent to a circle is a straight line which touches the circle at only one point (so it does not cross the circle - it just touches it).
- A tangent to a circle forms a right angle with the circle's radius, at the point of contact of the tangent.
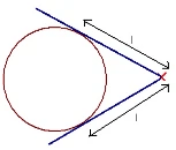
- Also, if two tangents are drawn on a circle and they cross, the lengths of the two tangents (from the point where they touch the circle to the point where they cross) will be the same.
4. Angle at the Centre

- The angle formed at the centre of the circle by lines originating from two points on the circle's circumference is double the angle formed on the circumference of the circle by lines originating from the same points.
- i.e. a = 2b.
5. Triangles Two Radii

- As both triangles have the same radii, it makes it an isosceles triangle.
6. Chord Bisector
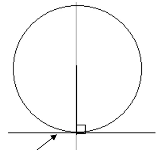
- A Chord is any line drawn across a circle. (Wherever it cuts it will always be 90 Degrees)
7. Cyclic Quadrilateral

- A Cyclic Quadrilateral is a 4-sided shape with every corner touching the circle.
- Both pairs of opposite angles add up to 180.
Alternate Segment Theorem
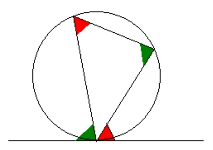
- This diagram shows the alternate segment theorem.
- In short, the red angles are equal to each other and the green angles are equal to each other.
When it comes to IGCSE/GCSE Maths, do you remember how to prove the alternate segment theorem?

- We use facts about related angles.
- A tangent makes an angle of 90 degrees with the radius of a circle, so we know that ∠OAC + x = 90.
- The angle in a semi-circle is 90, so ∠BCA = 90.
- The angles in a triangle add up to 180, so ∠BCA + ∠OAC + y = 180.
- Therefore 90 + ∠OAC + y = 180 and so ∠OAC + y = 90.
- But OAC + x = 90, so ∠OAC + x = ∠OAC + y.
- Hence x = y.
That's the end of the topic!

Drafted by Bonnie (Mathematics)

