IBDP Mathematics Question Analysis Topic: Mathematics - Circles
Exam Question:
Find the equations of the circle touching both axes and passing through the point (2,1).
Answer:
For IBDP Mathematics, you should know:
Assume a circle with a radius of r and a center at the coordinates (h,k).
Remember: the general equation of a circle is (x-h)2 + (y-k)2 = r2
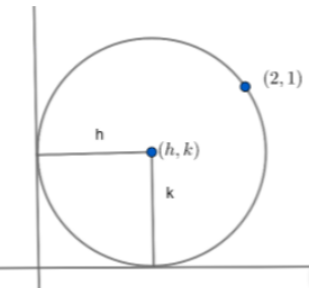
With the given information, we can plot the above diagram.
We can deduce that the radius of the circle is given by the above-drawn figure, which is r=h=k.
Therefore, the circle has a center of (h,h) and a radius of h.
Hence, the equation can be written as:
(x-h)2 + (y-h)2 = h2 (i) => x2 + h2 - 2hx + y2 + h2 - 2hy = h2
Simplified as:
x2 + y2 - 2hx - 2hy + h2 = 0 (ii)
Substituting x = 2 and y = 1 in equation (ii), we will find that h=5 and h=1.
Hence, by substituting these two values into equation (i) (separately), we will come up with the two equations:
(x-5)2 + (y-5)2 = 25 and (x-1)2 + (y-1)2 = 1
Work hard for your IBDP Mathematics examination!
End of analysis. Great!


