In this topic of IBDP Mathematics, we will be learning about the different forms of quadratic functions, the discriminant and how to use this information to sketch quadratic functions.
Quadratic Functions
In IBDP Mathematics, there are three different forms that the quadratic function can take - standard form, factored form and vertex form. Each way of representing the quadratic function provides different information, all of which can help us sketch the function.
Standard Form
- A quadratic function in standard form is given by y = ax2+bx+c.
- The following information about the quadratic function can be derived from standard form:
- The graph will cross the y-axis at (0,c) - this is the y-intercept
- The equation for the axis of symmetry is x = -b/2a. This value of x is also the x-coordinate of the vertex. You can then substitute this value of x into the quadratic to find the y-coordinate of the vertex.
- If a is greater than 0, then the shape of the parabola will be concave up (i.e. the parabola will be shaped like a U, with the vertex being the minimum point.)
- If a is less than 0, then the shape of the parabola will be concave down (i.e. the parabola will be shaped like an inverted U, with the vertex being the maximum point).
Factored Form
- A quadratic function in factored form is given by y = (x - p)(x - q).
- The following information about the quadratic function can be derived from factored form:
- The graph will cross the x-axis at (p,0) and (q,0) - these are the x-intercepts.
- The axis of symmetry is x = (p+q)/2.
- The graph will cross the y-axis at (0, -p * -q).
Vertex Form
- A quadratic function in vertex form is given by y = a(x - h)2 + k.
- The following information about the quadratic function can be derived from vertex form:
- The graph will have its vertex at (h,k)
- Like in standard form, the sign of a will determine the shape of the parabola. If a > 0, then the shape will be concave up. If a < 0, then the shape will be concave down.
One can manipulate the quadratic function from one form to another to acquire information about the quadratic function.
- To get from standard form to factored form, one can simply factor the quadratic.
- To get from factored form to standard form, expand out the brackets.
- To get from standard form to vertex form, complete the square.
- To get from vertex form to standard form, expand out the brackets.
- To get from vertex form to factored form (and vice versa), one would need to get the function back into standard form, and manipulate the function from standard form into either factored or vertex form.
Discriminant
In IBDP Mathematics, the discriminant provides information about the number of real roots (i.e. the number of real solutions to the quadratic equations). The number of real roots of a quadratic function tells us the number of x-intercepts the function has. .
- If a quadratic has two distinct, real roots, it will have two x-intercepts.
- If a quadratic has one repeated root, it will have one x-intercept.
- If a quadratic has no real roots, it will not have any x-intercepts.
The discriminant comes from the quadratic formula. As a reminder, the quadratic formula is given as follows:
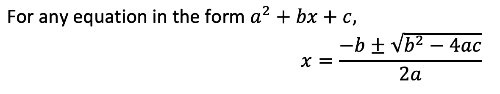
The one key part of the quadratic formula is the √b2 - 4ac. If we take a moment to think about it, the value of b2 - 4ac determines whether there are real solutions to the quadratic equation. If the value of b2 - 4ac is less than 0, then, because we are not allowed to square root negative numbers, then the equation will have no real solution - instead, it has complex solutions.
Because of the importance of this part of the quadratic formula in determining whether the equation has real roots/solutions, this part of the formula is given its own name - it is known as the discriminant (represented by △). Hence, the discriminant △ = b2 - 4ac.
- If △ > 0, then the quadratic has two distinct, real roots.
- If △ = 0, then the quadratic has one, repeated root.
- If △ < 0, then the quadratic has no real roots.
Sketching Quadratic Functions
In IBDP Mathematics, you will be expected to be able to sketch the graph of quadratic functions when given a quadratic function in either standard, factored or vertex form. Your sketch must include:
- Labelled x- and y-axis.
- y-intercepts and x-intercepts, with the coordinates labelled.
- The vertex, with its coordinates labelled.
- The axis of symmetry, with the equation of the line labelled.
- Correct shape of the parabola, with the parabola being symmetrical around the axis of symmetry.
With these tips and a bit of practice, you should be able to quickly and accurately sketch the graph of a quadratic function.
This is the end of this topic!


