This session shows the method to transform the graph of functions in I/GCSE Mathematics.
Transforming graphs of functions
In I/GCSE Mathematics, graphs can be transformed by shifting & stretching them.
The equation of the transformed graph will be related to the equation of the original graph.
When investigating transformations it is most useful to express functions using function notation.
For example, suppose we wish to investigate transformations of the function f(x) = x2.
The equation of the graph of y = x2, can be written as y = f(x).
Vertical translations
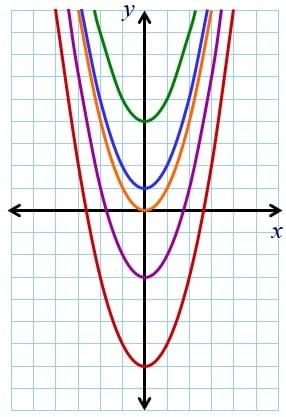
Below is the graph of y = x2, where y = f(x).
The blue one is the graph of y = f(x) + 1. and the green one is the graph of y = f(x) + 4.
The graph of y = f(x) + a is the graph of y = f(x) translated by the vector (0,a)
This purple is the graph of y = f(x) – 3 and the red one is the graph of y = f(x) – 7.
The graph of y = f(x) - a is the graph of y = f(x) translated by the vector (0,-a)
Horizontal translations
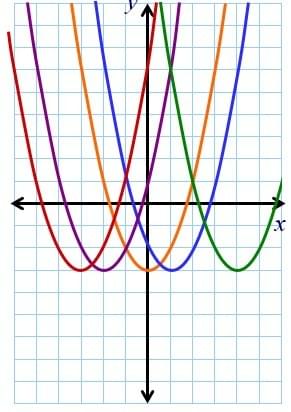
In I/GCSE Mathematics, below is the graph of y = x2, where y = f(x).
The blue one is the graph of y = f(x-1) . and the green one is the graph of y = f(x-4).
The graph of y = f(x+a) is the graph of y = f(x) translated by the vector (-a,0)
This purple is the graph of y = f(x+2) and the red one is the graph of y = f(x+3).
The graph of y = f(x-a) is the graph of y = f(x) translated by the vector (a,0)
Reflections in the x-axis
In I/GCSE Mathematics, establish that the graph of y = –f(x ), is a reflection of y = f(x) in the x-axis.
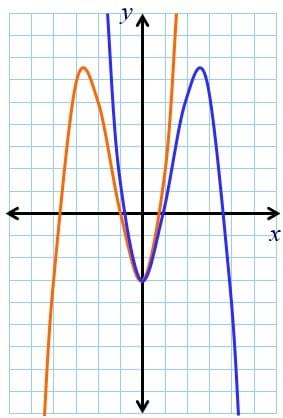
Below is the graph of y = x2 –2x – 2, where y = f(x).
The blue one is the graph of y = f(-x).
The graph of y = –f(x) is the graph of y = f(x) reflected in the x-axis.

Reflections in the y-axis
Establish that the graph of y = f(-x), is a reflection of y = f(x) in the x-axis.
Below is the graph of y = x3 –4x2 – 3, where y = f(x).
The blue one is the graph of y = f(-x).
The graph of y = –f(x) is the graph of y = f(x) reflected in the y-axis.
You finish reading the completing transformation of graph in I/GCSE Mathematics.
Well done!


