This is a method of finding some parameters inside a triangle in I/GCSE Mathematics.
The Cosine Rules
In I/GCSE Mathematics, the Cosine rule can be used to find:
- An unknown side when two sides of the triangle and the included angle are given.
- An unknown angle when 3 sides are given.
For finding an unknown sides a, the equation will be defined as
a2 = b2 + c2 – 2bcCosA
For finding an unknown angles the 3 formula for sides need to be re-arranged in terms of Cos A, B or C.
2bcCosA = b2 + c2 – a2
CosA = b2 + c2 – a2 / 2bc
Therefore, applying the same method as earlier to the other sides produce similar formulae for b and c, namely:
b2 = a2 + c2 – 2acCosB
c2 = a2 + b2 – 2abCosC
Therefore, applying the same method as earlier to the other angles produce similar formulae for b and c, namely:
CosB = a2 + c2 – b2 / 2ac
CosC = a2 + b2 – c2 / 2ab
To find an unknown side we need 2 sides and the included angle.
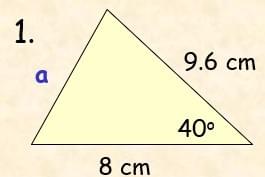
a2 = 82 + 9.62 – 2 x 8 x 9.6 x Cos 40o
a = SqRoot(82 + 9.62 – 2 x 8 x 9.6 x Cos 40o)
a = 6.2 cm (1 dp)
In I/GCSE Mathematics, to find an unknown angle we need 3 given sides.

CosA = (82 + 9.62 – 6.22 )/ (2 x 8 x 9.6)
A =40o
You finish reading and completing in cosine rule in I/GCSE Mathematics.
Well done!


