This session shows the method of direct proportion in I/GCSE Mathematics.
Direct proportion
If two quantities increase at the same rate so that if one is doubled so is the other, then the quantities are said to be directly proportional.
In the example shown, if C is the cost of an ice cream and N is the number bought, we write C µ N (C is proportional to N).
In I/GCSE Mathematics, if two quantities are directly proportional then their points lie on a straight line from the origin. In our example the equation of this line is C = kN for some value of k. k is called the constant of proportionality and has a value of 1.5 here.
Terminology
Strategy for solving proportion problems
1. Find the value of k (the constant of proportionality).
2. Use k together with given values to answer the question.
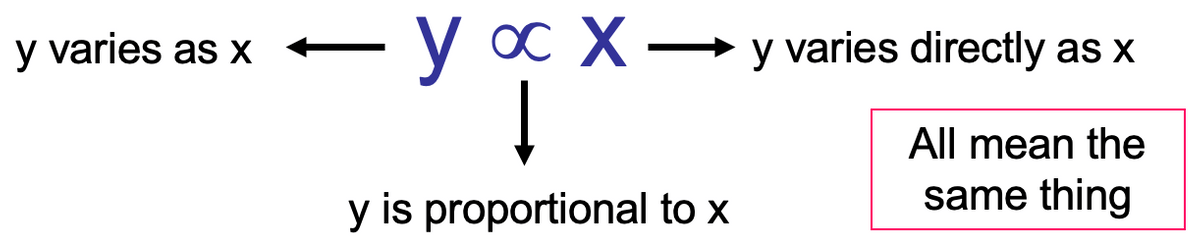
Example 1:
If y is proportional to z and y = 7 when z = 2, find:
(a) the value of y when z = 8
(b) the value of z when y = 10.5
y = kz
k = y/z
k = 7/2 = 3.5
y = 3.5z
(a) y = 3.5 x 8 = 28
(b) z = y/3.5 = 10.5/3.5 = 3
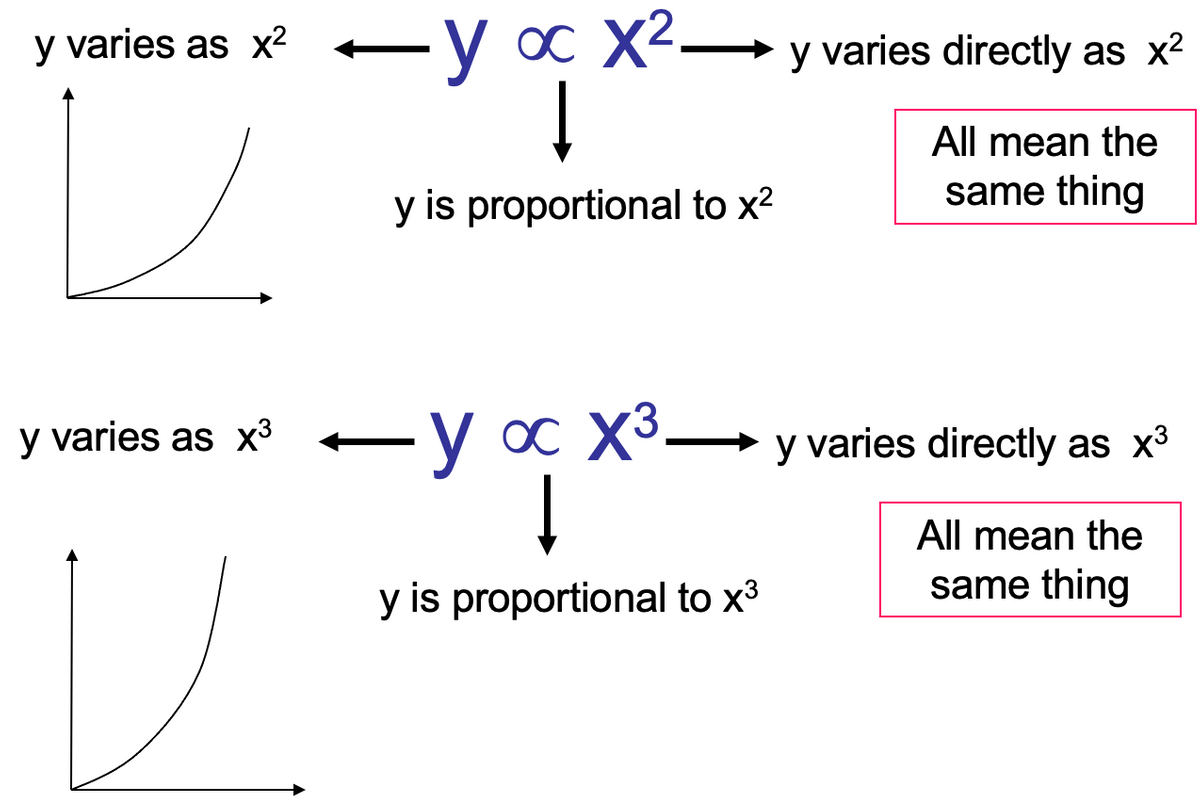
Questions Involving Squares and Cubes
When it comes to I/GCSE Mathematics, One quantity can be proportional to the square or cube of another.
Example 2 :
The energy of a moving body E, is proportional to the square of its speed S. If a body has 90 units of energy when it is moving at 3m/s, calculate:
(a) How many units of energy it has at a speed of 8 m/s.
(b) The speed of a body with 810 units of energy.
E = kS2
k = E/S2
k = 90/32 = 10
E = 10S2
(a) E = 10 x 82 = 640 units
(b) S = (E/10) = (810/10) = 9 m/s
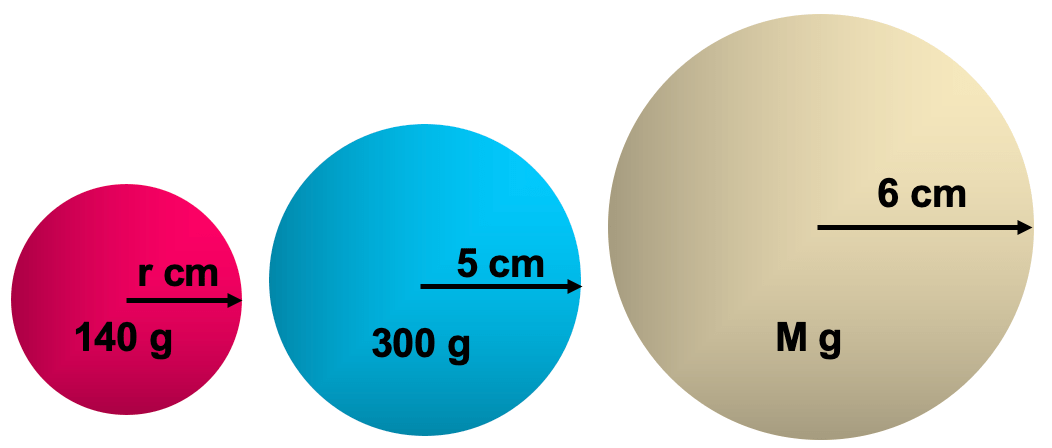
Example 3 :
The mass M of a sphere is proportional to the cube of its radius r. Use the information in the diagram to find:
(a) The mass of the yellow cube.
(b) The radius of the red cube.
M = kr3
k = M/r3
k = 300/53 = 2.4
M = 2.4r3
(a) M = 2.4 x 63 = 518.4 g
(b) r = 3 (M/2.4) = 3 (140/2.4) = 3.9 cm (1 dp)
You finish reading .
Well done!


