AS/A-level Physics: Terminal Velocity & Viscous drag

In this chapter of AS/A-level Physics, we will learn about Terminal Velocity & Viscous drag.

𝑎 = ∑ 𝐹/𝑚

In AS/A-level Physics, From this, we can calculate the resulting acceleration for falling objects; we need to include WEIGHT, UPTHRUST caused by the object being fluid in air and the VISCOUS DRAG force caused by the movement. The changing velocity makes the viscous drag difficult to calculate, so we consider the equilibrium situation, in which the weight exactly balances the sum of upthrust and drag, meaning that the falling velocity remains CONSTANT, thus it is the TERMINAL VELOCITY.

In AS/A-level Physics, Viscous drag is the friction force between a solid and a fluid. Calculating this can be simple, so long as it is a SMALL REGULARLY SHAPED OBJECT (otherwise it is difficult as the turbulent flow creates and unpredictable situation)

Stokes’ Law

Viscous drag (F) on a small sphere at low speeds:

F= 6πrȠv

r – Radius of the sphere (m)

v – Velocity of the sphere (ms^-1)

Ƞ - coefficient of viscosity of the fluid (Pa s)

In such a situation, the drag force is directly proportional to the radius of the sphere and directly proportional to the velocity, neither of which is necessarily an obvious outcome.

In AS/A-level Physics, Consider this: a ball bearing is dropped through a column of oil

Terminal velocity: weight = upthrust + stokes’ law

𝑚_𝑠𝑔 = 𝑤𝑒i𝑔ℎ𝑡 𝑜ƒ ƒ𝑙𝑢i𝑑 𝑑i𝑠𝑝𝑙𝑎𝑐𝑒𝑑 + 6𝜋𝑟 𝑣_{𝑡𝑒𝑟𝑚}

M_s is the mass of the sphere and v_term is the terminal velocity

Mass of the sphere, m_s: 𝑚_𝑠 = 𝑣𝑜𝑙𝑢𝑚𝑒 𝑥 𝑑𝑒𝑛𝑠i𝑡𝑦 𝑜ƒ 𝑠𝑝ℎ𝑒𝑟𝑒 = 4/3 𝜋𝑟³ 𝑥 𝜌_𝑠

Weight of the sphere, W_s: W_𝑠 = 𝑚_𝑠𝑔 = 4/3 𝜋𝑟³𝜌_𝑠𝑔

For the sphere, the upthrust = weight of fluid displaced

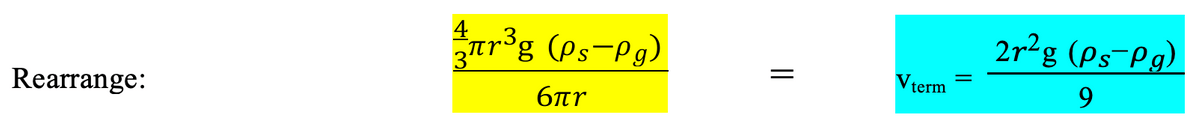
Terminal velocity is proportional to the square of the radius. Therefore, a larger sphere falls faster. More complex situations have more complex equations. This isn’t however a common situation, however the principle that larger objects generally fall faster holds true for most objects without a parachute.

That's all~ Thanks for watching.