Density (p) is measured in kg m-3. It can be calculated using the equation below;
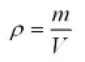
- p = density in kg m-3
- m = mass in kg
- V = volume in m3
Hooke’s Law
- The extension of a spring or wire is directly proportional to the force applied provided the limit of proportionality is not exceeded.
- When a graph of force against extension is plotted for a material which obeys Hooke’s law it looks like the graph below.
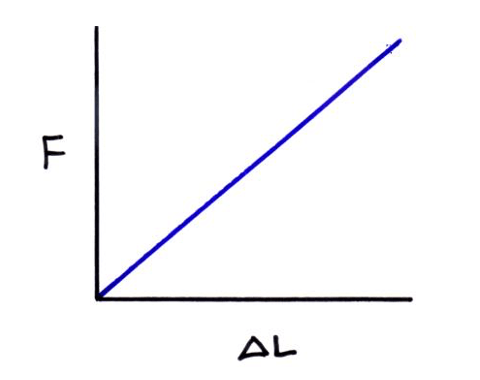
- The gradient of this graph is the spring constant (k) which is measured in Nm-1.
- F = force in newtons (N)
- ΔL = change in length in metres (m)
- k = spring constant (N m-1)
- Note that in AS/A- level physics exam, the limit of proportionality is the point beyond which Hooke’s law is no longer true when stretching a material.
- The elastic limit is the point beyond which the material you are stretching becomes permanently stretched so that the material does not return to its original length when the force is removed.
Stress & Strain
Stress
- The stress applied to a material is the force per unit area applied to the material. The maximum stress a material can stand before it breaks is called the breaking stress or ultimate tensile stress.
- Tensile means the material is under tension. The forces acting on it are trying to stretch the material. Compression is when the forces acting on an object are trying to squash it.
- The equation below is used to calculate the stress.
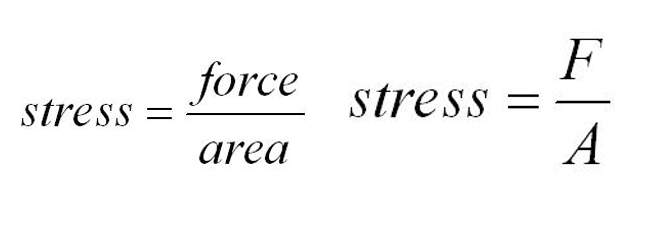
- stress = stress measured in Nm-2 or pascals (Pa)
- F = force in newtons (N)
- A = cross-sectional area in m2
Strain
The ratio of extension to original length is called strain it has no units as it is a ratio of two lengths measured in metres.
- strain = strain it has no units
- ΔL =extension measured in metres
- L = original length measured in metres
Stress-Strain graph for a ductile material (like copper)
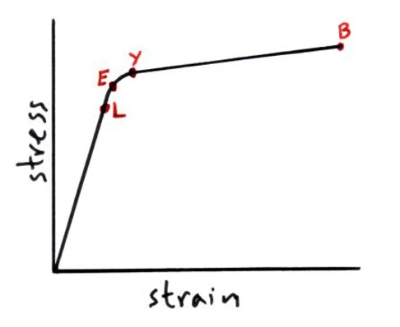
- L = the limit of proportionality, Hooke’s law applies up to this point.
- E = elastic limit, beyond this point the material is permanently stretch and it will not go back to its original length. Elastic behaviour is when a material returns to its original length, plastic behaviour is when the stretched material does not return to its original length.
- Y = yield point, beyond this point small increases in force give much big increases in length.
- B = breaking point / breaking stress, the material breaks at this point.
Stress-Strain graph for a brittle material (like glass)
Elastic strain energy (energy stored in a stretched wire or spring)
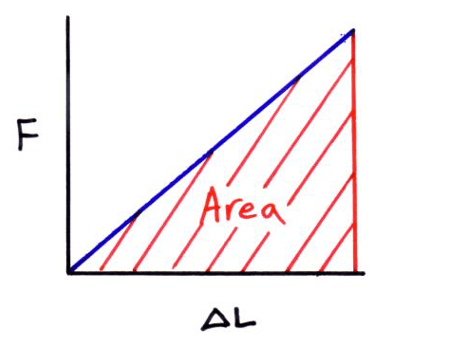
The energy stored in the stretch wire or spring is the area under the force-extension graph as we can see in the equation below.
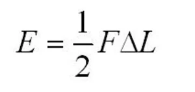
- E = elastic strain energy in joules (J)
- F = force in newtons (N)
- ΔL = change in length in metres (m)
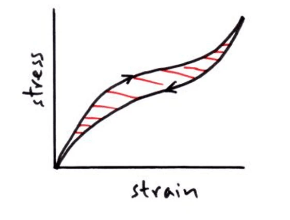
Stretching rubber
- When rubber is stretched and released energy is lost as heat and this is called hysteresis. The area between the two lines is the energy lost per unit volume.
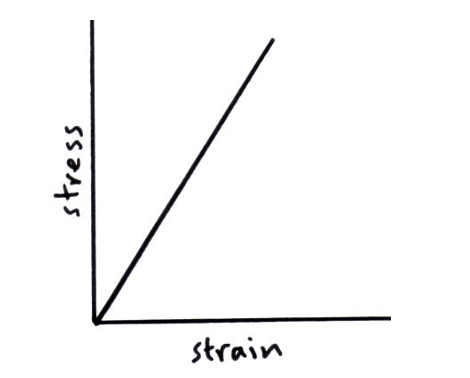
Young Modulus
What is a modulus?
- A modulus is a numerical value, which represents a physical property of a material .
What is the Young Modulus?
- It is the modulus of elasticity. This means it is a number which represents how easy it is to deform (stretch a material).
- When a material is stretched stress is directly proportional to strain provided it is not stretched beyond the limit of proportionality. The gradient of the graph below gives us the value of the Young Modulus for that particular material.
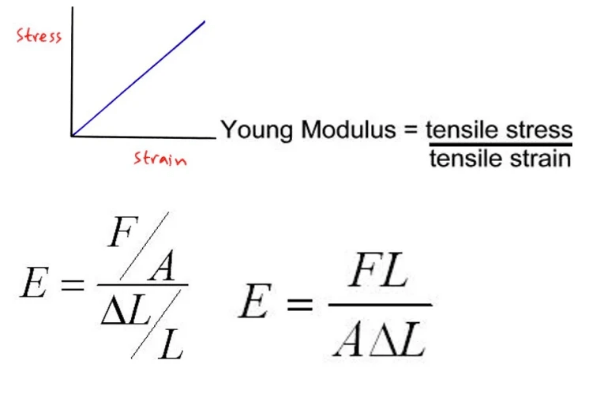
- E = the young modulus in pascals (Pa)
- F = force in newtons (N)
- L = original length in metres (m)
- A = area in square metres (m2)
- ΔL = change in length in metres (m)
Measurement of the Young Modulus
The Young Modulus for a wire can be measured using this equipment. The reference wire and test wire are hung from the ceiling. The reference wire supports a vernier scale which will measure the extension of the test wire. The force on the test wire can be varied using the slotted masses.
Measurements needed;
- 1) The original length of the test wire (L) should be measured with a tape measure.
- 2) The cross-sectional area (A) can be calculated from measuring the wires diameter with a micrometer. The micrometer should be used to measure the diameter at several different points along the wire.
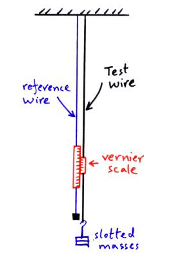
- 3) The test wire will have several different forces (F) applied using the slotted masses and each time the extension of the test wire (L) will be measured using the vernier scale.
- A graph of force against extension can be plotted from which the gradient can be calculated.
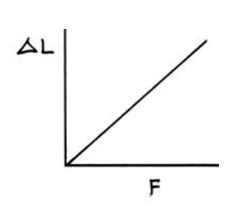
- The Young Modulus can then be calculated from the gradient using the equation below.
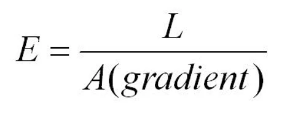
References:
- https://getrevising.co.uk/resources/as_physics_materials_notes
And we're all done for today!

Drafted by Kin (Physics)

