·
Capacitors
- A capacitor is an electronic component that can store electrical charge and then release it. It is made of two conducting plates separated by an insulator, which you will need to know for AS/A-level Physics. The charge that is stored by the capacitor is due to the potential difference across. We can write this as:
- Q ∝ V or Q = kV
- k is a constant specific to the capacitor, this is called the capacitance and is represented by the symbol C
- Q = CV
- Capacitance is measured in Farads, F, and charge is measured in Coulombs, C.
- We can rearrange the equation into C = Q / V and from this we can see that capacitance is a measure of the charge stored per volt of potential difference. 1 Farad means 1 Coulomb of charge is stored per Volt.

Water Analogy
- We can think of the charge stored by a capacitor as the volume of water in a bucket.
- The cross-sectional area of the bucket represents the capacitance of the capacitor. We can see that the capacitance of capacitor 1 is higher than the capacitance of capacitor 2.
- The height of the water represents the potential difference across the capacitor. We can see that the potential difference across capacitor 2 is higher than the p.d. across capacitor 1. The charge stored by both capacitors is the same.
- A capacitor with a lower capacitance can store more charge if the p.d. across it is increased.

Charging and Discharging
- When a capacitor is connected to a battery is sends out electrons to one of the plates, this becomes negatively charged. The same amount of electrons move from the second plate and enter the battery, leaving the plate positively charged. The capacitor is now storing a charge or is ‘charged’.
- If the charged capacitor is disconnected from the battery and connected to a lamp it will give out the stored charge or will ‘discharge’, and this is an important topic in AS/A-level Physics. The electrons on the negative plate move through the circuit and onto the positive plate. The plates now have no charge on them. The energy stored by the capacitor is transferred to the bulb whilst the electrons move (whilst a current flows).
Energy Stored by a Capacitor
- The top equation shows us that the charge of a capacitor increases with the potential difference across it. If we plotted p.d. against charge we get a graph that looks like this
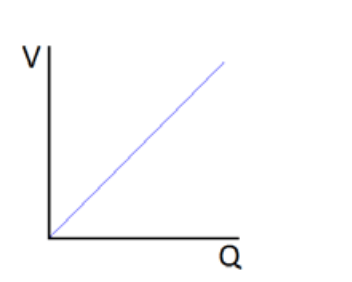
- We can derive an equation to find the energy that a capacitor stores by considering the energy transferred during the shaded section on the lower graph.
- In this section the charge changes from q to q+Δq when an average p.d. of v is applied across it.
- Using E = VQ (see AS Unit 1) the energy stored is E= vΔq.
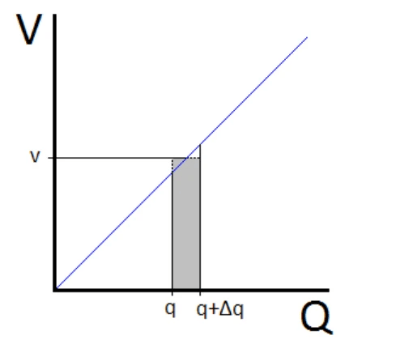
- The total energy is equal to the total of all the little rectangular sections and is given by E = ½ QV. This is also equal to the area under the graph.
- We can use the top equation to derive two more equations for the energy stored by a capacitor:
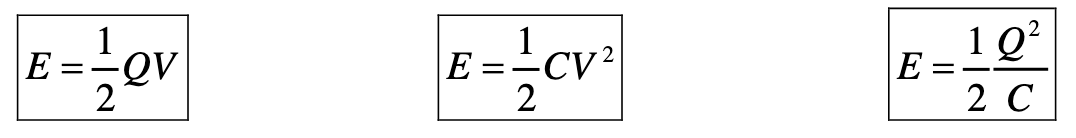
Energy is measured in Joules, J
Charging and Discharging
In the diagram to the right a capacitor can be charged by the battery if the switch is moved to position A. It can then be discharged through a resistor by moving the switch to position B.
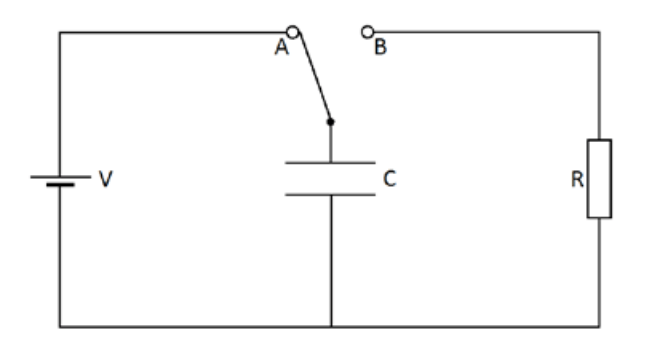
- Charging a Capacitor - When the switch is moved to A the battery sends electrons to the lower plate and takes them from the upper plate. This leaves the lower plate negatively charged and the upper plate positively charged. An electric field is set up between the plates.
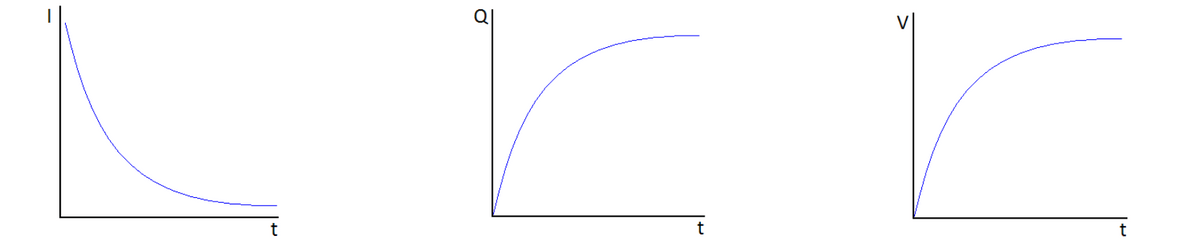
- Current - The current is the flow of electrons through the circuit (see Unit 1). There is a large current initially as electrons move to the lower plate. As time passes and more electrons are on the plate it becomes more difficult to add more due to the electrostatic repulsion of similar charges. When no more electrons move in the circuit the current drops to zero.
- Charge - The charge stored by the capacitor increases with every electron the moves to the negative plate. The amount of charge increases quickly at the beginning because a large current is flowing. As the current drops the rate at which the charge increases also drops. A maximum charge is reached.
- P.D. - Since potential difference is proportional to charge, as charge builds up so does p.d. The maximum value of p.d. is reached as is equal to the terminal p.d. of the battery.
- Discharging a Capacitor - When the switch in moved to B the electrons on the negative plate repel each other and move back into the circuit. Eventually both plates lose their charge and the electric field between them disappears.
- Current - There is initially a large current as the electrons leave the negative plate. As the number of electrons on the negative plate falls so does the size of the repulsive electrostatic force, this makes the current fall at a slower rate. When no more electrons move in the circuit the current drops to zero.
- Charge - The charge that was stored on the plates now falls with every electron that leaves the negative plate. The charge falls quickly initially and then slows, eventually reaching zero when all the charge has left the plates.
- P.D. - As the charge falls to zero so does the potential difference across the capacitor.

Time Constant, τ
- The time it takes for the capacitor to discharge depends on the ‘time constant’.
- The time constant is the time it takes for the charge or p.d. of a capacitor to fall to 37% of the initial value. OR
- The time constant is the time it takes for the charge or p.d. of a capacitor to fall by 63% of the initial value.
- It is given by the equation: τ = RC
- If the capacitor has a larger capacitance it means it can hold more charge, this means it will take longer to discharge. If the resistor has a larger resistance it means it is harder to move the electrons around the circuit, this also means it will take longer to discharge.
Exponential Decay
Finding τ from Graphs
- The time constant of a discharging capacitor can be found from a graph of either charge, current or potential difference against time. After one time constant the value will have dropped to 0.37 of the initial value.
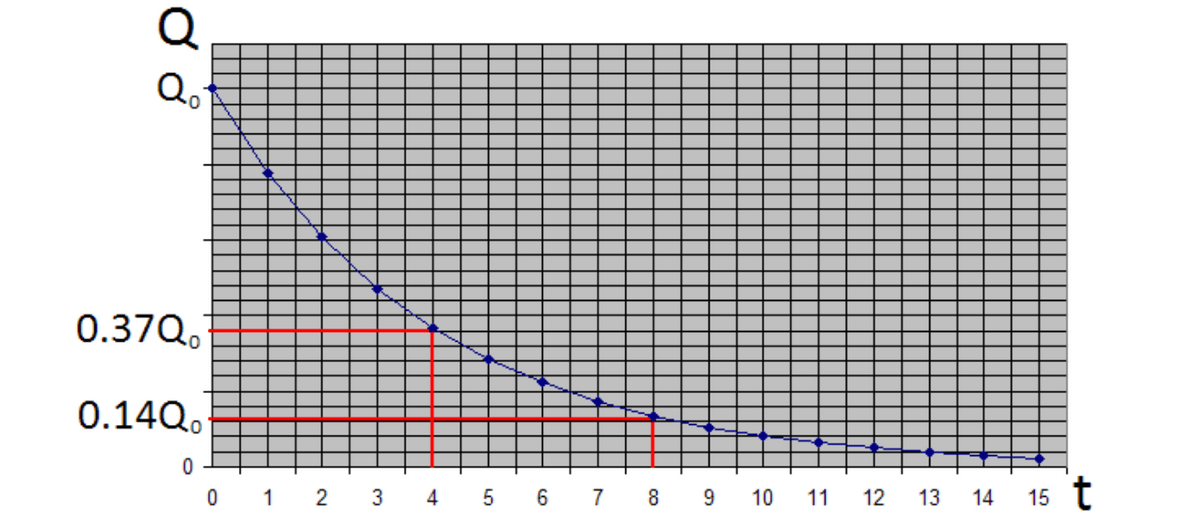
- In this case the time constant is 4 seconds.
Quantitative Treatment
- We could use the graph above to find the charge on the capacitor after a time, t. We could also use it to find the time it takes for the charge to fall to a value of Q.
- This requires the graph to be drawn very accurately and values need to be taken from it very carefully.
- Instead of doing this we can use the following equation to calculate the charge, Q after a time, t.
- t is the time that has elapsed since discharge began
- Q is the remaining charge
- Q0 is the initial (or starting) charge
- RC is the time constant, also equal to the resistance multiplied by the capacitance.
- When the time elapsed is equal to the time constant the charge should have fallen to 37% of the initial value.
- When the time elapsed is equal to twice the time constant the charge should have fallen to 37% of 37% of the initial value.
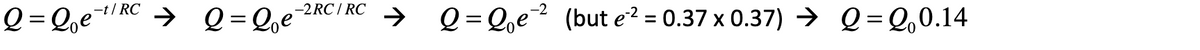
- Similar equations can be established for the current flowing through and the potential difference across the capacitor after time, t:
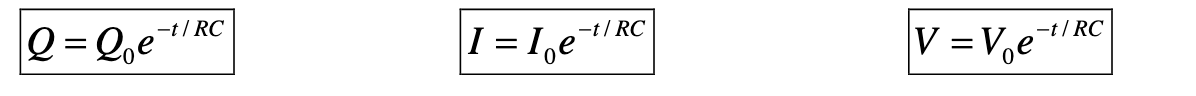
Rearrangment
The equations above can be rearranged to make t the subject. We will use the equation for charge:

They can also be rearranged to make RC (time constant) the subject:
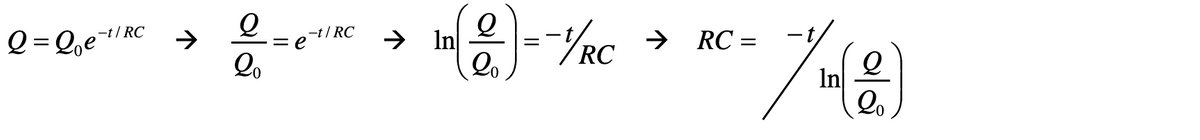
References
- https://getrevising.co.uk/resources/a2-notes-capacitors
- https://thumbs.gfycat.com/FlamboyantFatHectorsdolphin-max-1mb.gif
- https://f00.psgsm.net/content/12893/article.jpg
That's all for this one!

Drafted by Kin (Physics)

