Sometimes you may need to use the ‘trapezium rule’ to approximate the area beneath a curve which is very hard to Integrate. Let's learn about it in A-Level Maths!
Trapezium rule
Imagine we had a curve as shown to the right, and we wanted to find the area in the region indicated
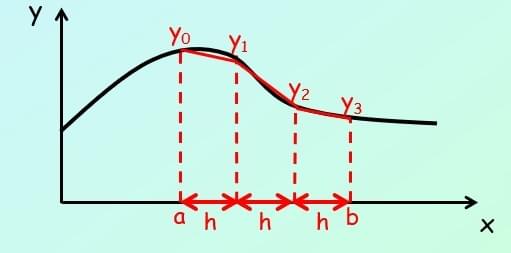
We could split the region into strips, all of the same height (in this case 3), and work out the area of each strip as a trapezium
We could then add them together and the area would be an approximation for the area under the curve
If we want a better approximation, we just need to use more strips…
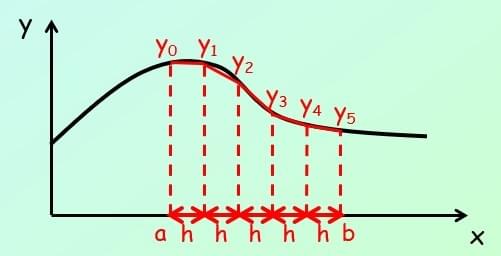
Let's see what the algebra would look like for using the trapezium rule in a question…
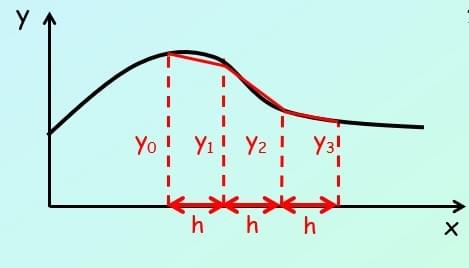
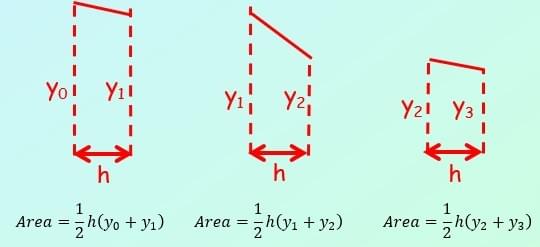
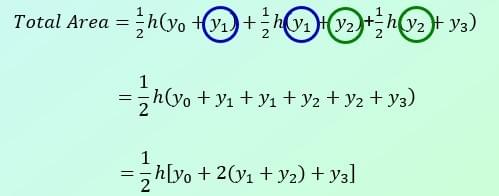
The rule
As a general case, the trapezium rule looks like this:
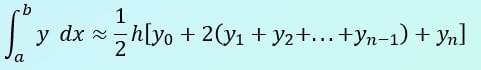
and h = (b - a) / n
The height of each strip is given by the difference between the limits, divided by‘n’, the number of strips…
Example:
Using 4 strips, estimate the area under the curve:
y=√(2x+3)
Between the lines x = 0 and x = 2
You will not need to integrate at all to do this
Start by finding the height of each strip…
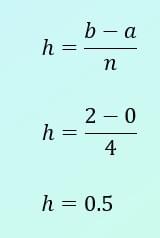
Now draw up a table and work out y values at the appropriate x positions between 0 and 2…

For each of these values of x, calculate the value of y by substituting it into the equation of the curve
Now sub the values you worked out into the formula – the first value for y is y0 and the last is yn

Another example:
Using 8 strips, estimate the area under the curve:
y=√(2x+3)
Between the lines x = 0 and x = 2
Height = (2 - 0) / 8
=0.25
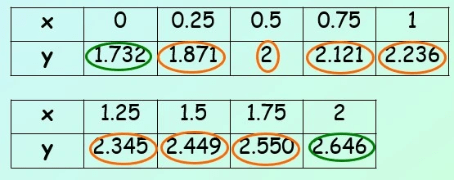

Note that this will be a better estimate as the area was split into more strips!
Drafted by Eunice (Maths)

