Integration is a way of adding slices to find the whole. Let's learn about it in A-Level Maths.
Integration can be used to find areas, volumes, central points and many useful things. But it is easiest to start with finding the area between a function and the x-axis like this:
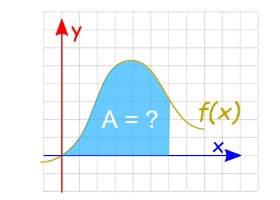
Finding an Integral is the reverse of finding a derivative.

Notation
The symbol for "Integral" is a stylish "S" (for "Sum", the idea of summing slices):
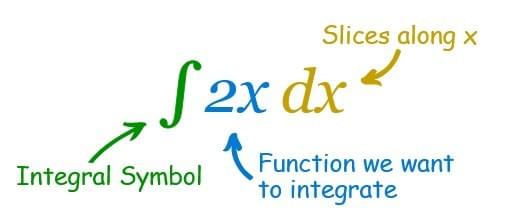
After the Integral Symbol we put the function we want to find the integral of (called the Integrand), and then finish with dx to mean the slices go in the x direction (and approach zero in width).
And here is how we write the answer:
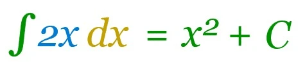
Plus C
It is the "Constant of Integration". It is there because of all the functions whose derivative is 2x:
- the derivative of x2 is 2x,
- and the derivative of x2+4 is also 2x,
- and the derivative of x2+99 is also 2x,
- and so on!
Because the derivative of a constant is zero.
So when we reverse the operation (to find the integral) we only know 2x, but there could have been a constant of any value.
So we wrap up the idea by just writing + C at the end.
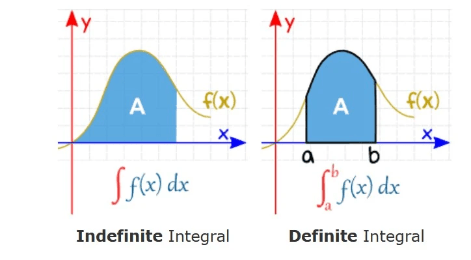
Definite vs Indefinite Integrals
A Definite Integral has actual values to calculate between (they are put at the bottom and top of the "S"):
Drafted by Eunice (Maths)
Reference
https://www.mathsisfun.com/calculus/integration-introduction.html

