Let's learn how to use definite Integration to find areas under curves in A-Level Maths!
Definite integral and area
To find the area under a curve, between two values of x, you follow the process of definite integrals.
The values of a and b will be the limits of the Area, and y is the function of the curve.
Itis important to note that when we say ‘the area under the curve’, this means the area between the curve and the x-axis.
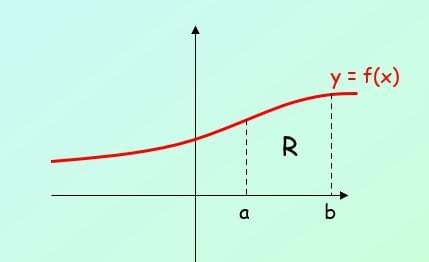
Example Question
Find the value of R, where R is the area between the values of x = 1 and x = 3, and under the following curve:
y= x2 + 4/x2

Area under the x-axis
Find the area of the finite region bounded by the curve y = x(x – 3) and the x-axis
1. Start with a sketch…
2. The graph will cross the x-axis at 0 and 3…
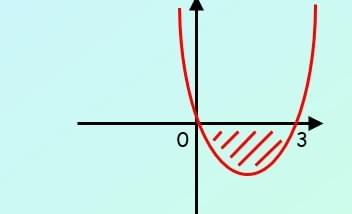

So the area is 4.5 square units (you can write is as a positive value…)
Area both above and below x-axis
Find the area between the curve:
y= x(x + 1)(x – 1) and the x-axis
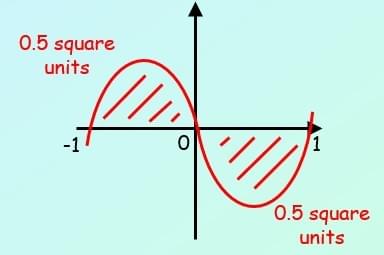
You need to integrate each section separately and then combine them (as positive values…)
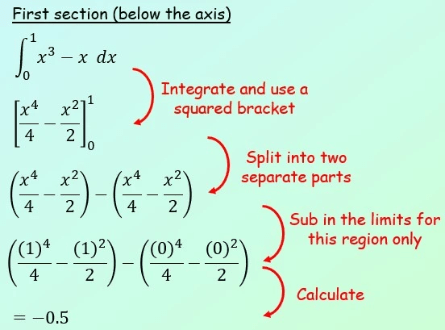

The total area is therefore 1 square unit.
Drafted by Eunice (Maths)
Reference
https://www.mathsisfun.com/calculus/integration-definite.html

