In this chapter of AS/A-Level Chemistry, we will learn about rate of reaction and activation energy.
Activation Energy
We can calculate the activation energy using the Arrhenius equation:
k = Ae_Ea/RT
Where;
k = rate constant EA = activation energy (J)
T = temperature (K) R = gas constant (8.31 JK-1mol-1)
A = another constant
Some relationships to note:
- As EA increases, k will get smaller. Therefore, large activation energy, means a slow rate – this makes sense!
- As T increases, k increases. Therefore at high temperatures, rate will be quicker – this makes sense too!
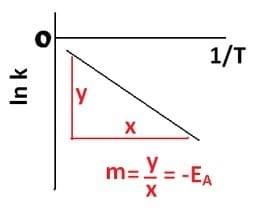
If we “ln” both sides of Arrhenius’ equation, we get;
ln k = – EA/RT + ln A
This looks a bit like:
y = mx + c
If we plot ln k (y) against 1/T (x), the gradient we produce will be –EA/R (m). Then R is just a number that we know (8.31 JK-1mol-1) we can rearrange and find the activation energy in AS/A-Level Chemistry.
Iodine clock reaction
e can use iodine clock reaction as an example to demonstrate the calculation under the AS/A-Level Chemistry.
S2O82- (aq) + 2I- (aq) —> 2SO42- (aq) + I2 (aq)
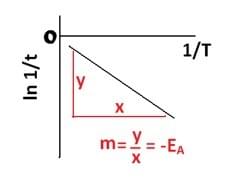
Rate of reaction is inversely proportional to the time taken for the solution to change colour
i.e. increased rate = decreased time taken
k α 1/t
We can say that 1/t is the same as k (rate constant) and we can substitute 1/t instead of k in Arrhenius’ equation and find the gradient again to find a value for EA
Congratulations! Now you understand the calculation of activation energy in AS/A-Level Chemistry.


