Do you still remember the kinetic theory of gases in A2/A-level Physics?
Ideal Gases
- Avogadro’s constant is the number of atoms/particles in one mole of a substance and is 6.02x1023.
- One mole of a substance is the amount which contains the same number of particles as there are in 12g of Carbon-12.
There is a model for the kinetic theory of gases, which includes a number of assumptions including:
(1) The forces between atoms are negligible except for during collisions.
(2) Collisions are perfectly elastic, and the time of collisions is negligible compared with the time between collisions.
(3) The volume of occupying atoms/particles is negligible compared with the volume of the container.
(4) There are a large number of atoms/particles in a random, rapid motion.
Pressure
- Pressure is defined as being the forces exerted per unit surface area.
- When in a container, particles move in a random, rapid motion, and perform perfectly elastic collisions with the walls of the container.
- During these collisions, a force is exerted onto the wall as an impulse due to Newton’s third law of motion.
- The force on the walls of the container is defined as being the rate of change of momentum and this force can be divided by the total surface area to give the pressure exerted on the container.
- Boyle’s law states that the pressure exerted by a fixed mass of gas is inversely proportional to the volume, providing that the temperature remains constant.
pV = Constant or p1V1 = p2V2
- The gas law tells us that pressure is directly proportional to temperature providing that volume remains constant.
p/T = Constant
- Charles’ Law expresses that volume and temperature are directly proportional given that pressure remains constant.
V/T = Constant
- The Combined gas law is as follows:
(p1V1)/T1 =(p2V2)/T2
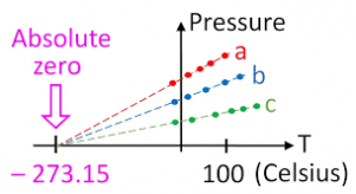
- From the gas law, Pressure and Temperature which are directly proportional can be used to determine the value for Absolute Zero.
- The equipment is set up as shown with the pressure and temperature recorded at regular intervals using the pressure gauge and thermometer.
- The values for pressure and temperature can then be plotted onto a graph, and the graph extrapolated until the point at which it crosses the x axis.
- The value at the X axis gives us the value for absolute zero as at zero temperature, there is theoretically zero pressure due to minimal internal energy and so no forces acting in any given direction on any given surface area.
- This value should come out at -273ᵒC.

The equation of state of an ideal gas is given by the equation:
pV=nRT
Whereby n=number of mols, R=Molar gas constant of 8.31 JK-1mol-1, T=Temperature.
- In a gas, the average velocity would be 0ms-1, due to velocities being vector quantities.
- Therefore, we use the root mean square speed (r.ms.).
- This is the square of the velocity of each atom and then the average of the squared values are found.
The mean square speed is determined for use in the equation:
pV=1/3 Nm(c^2 ) ̅
With N= Number of atoms.
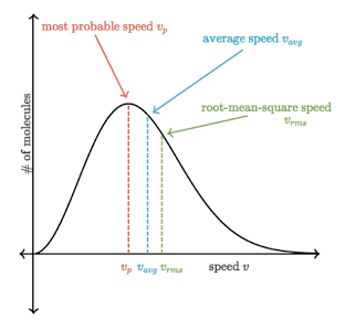
- The Maxwell-Boltzmann distribution shows us the range of speeds of the particles in a gas at a given temperature as shown in the graph.
- The Boltzmann Constant, K, is given by
k = R/NA = (8.31JK^(-1) mol^(-1)) / (6.02×10^23 mol^(-1) ) = 1.38×10^(-23) JK^(-1)
And can be used in the equations: 1/2 m(c^2 ) ̅= 3/2 kT
- For an ideal gas, the assumptions of the kinetic model of an ideal gas, states that the electrostatic forces between particles are negligible and so therefore there is no potential energy in an ideal gas, all of the internal energy is in the form of kinetic energy.
- Doubling the temperature of an ideal gas doubles the average kinetic energy and so doubles the internal energy.
That's the end of the topic!

Drafted by Bonnie (Physics)

