Do you still remember gravitational fields in A2/A-level Physics?
Gravitational Fields
- A gravitational field exists around any mass, no matter how large or small.
- Other masses in this region will feel a force, which is always attractive: a repulsive gravitational force has never been identified.
Gravitational Field Lines
- Gravitational fields are always drawn using gravitational field lines, which show the direction of the force on a mass placed at any point in the field.
- Around a spherical mass the lines look like this:

- Near the Earth’s surface, the field is nearly uniform and the lines are evenly spaced.

Gravitational Field Strength, g
The gravitational field strength g at a point in a field is the force per unit mass on an object placed at that point.
g= F/m
- It follows from Newton’s universal law of gravitation that, around a spherical mass M:
g=G M/r²
Where r is the distance from the centre of the mass.
- g has units Nkg¯¹.
- g may also be regarded as the acceleration due to gravity (ms¯²) at the point.
- g is a vector quantity.
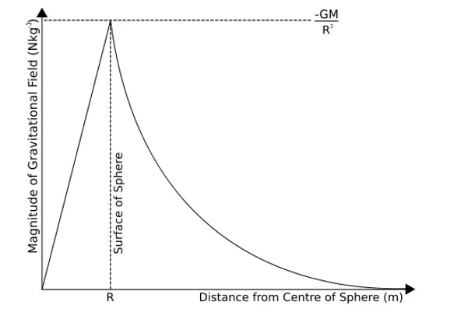
- The variation of g with distance from a mass is another inverse-square relationship.
Earth’s Gravitational Field
- It’s strength is 9.81Nkg¯¹ at the surface of the Earth.
- It falls off with distance above and below the surface.
Gravitational Potential, V
When a mass is moved against a gravitational force, work is done.
This is described using the concept of gravitational potential, V, defined as the work done in taking unit mass from infinity to a point in a field.
Thus, at a distance r from a mass M, it can be shown that:
V=G M/r
- V is a scalar quantity.
- V is zero at infinity.
- At all other places, V is negative (since a negative amount of work has to be done to move a mass against an attractive force).
- The gravitational field strength is equal to the potential gradient (slop of a graph V against r).
Escape Velocity
If a mass at the Earths surface can be given a kinetic energy equal to its gravitational potential energy (mV), it will escape completely from the Earth’s gravitational field.
The velocity required to do this is called the escape velocity, it is not dependent on the mass and is given by:
v= √(2GM/r)= √((2gr))
Equipotential Surfaces
- Points that are at the same potential lie on equipotential surfaces.
- Around a spherical mass, these are concentric spheres – or circles in two dimensions.
- Equipotential surfaces are always perpendicular to field lines.
That's the end of the topic!

Drafted by Bonnie (Physics)

