Round and Round:
In A2/A-level physics exam, objects moving in a circle with a constant speed must have a force acting on it, directed towards the centre of the circle. This is called the centripetal force. It is not a specific force, but a name given to force that causes an object to stay in circular motion. Common examples of centripetal force are: normal reaction, weight, tension, or components of these forces.
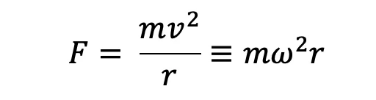
- F = Centripetal Force
- m = Mass
- v = Constant Linear Velocity
- r = Radius of Circle
- ω = angular velocity
An object in circular motion is constantly accelerating
- Acceleration is rate of change of velocity
- Velocity is speed in a given direction
- Object is constantly changing direction, therefore constantly accelerating
- Direction is always a tangent to the circle
Angular Velocity (ω)
- Angular Velocity is the rate of change of angle with time
- Measured in radians
- 2π radians=360 degrees
- Measured in radians
- When an object moves at a steady speed along the arc of a circle or radius r travelling a distance s in a time t
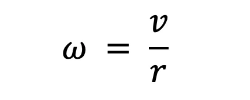
- v = Velocity
- r = Radius
- ω = angular velocity
Period and Frequency
- The time period (T) of an oscillation is related to the frequency (f) by the equation
- T=1/f
- T is time taken for full circle
- Showing the objects steady angular speedcan be found from
- T= 2π/ω
Back and Forth
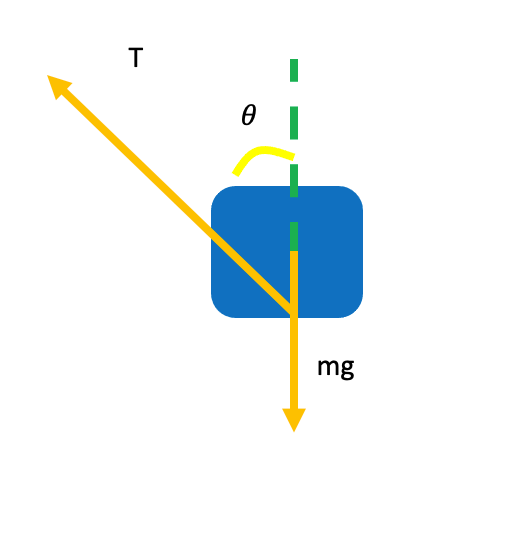
On a swing, the centripetal force is provided by the difference between the seat reaction (R) and the rider’s weight (mg)
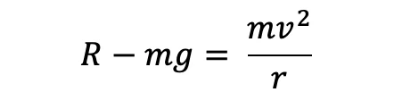
Reaction of the seat on the rider is then given by
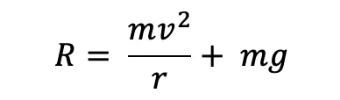
During the revolution at angle θ
- Reaction force is given by
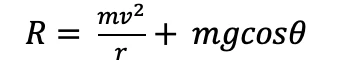
- As cos θ is less than one this means that the reaction force decreases, therefore acceleration and thrill
Funfair Rides:
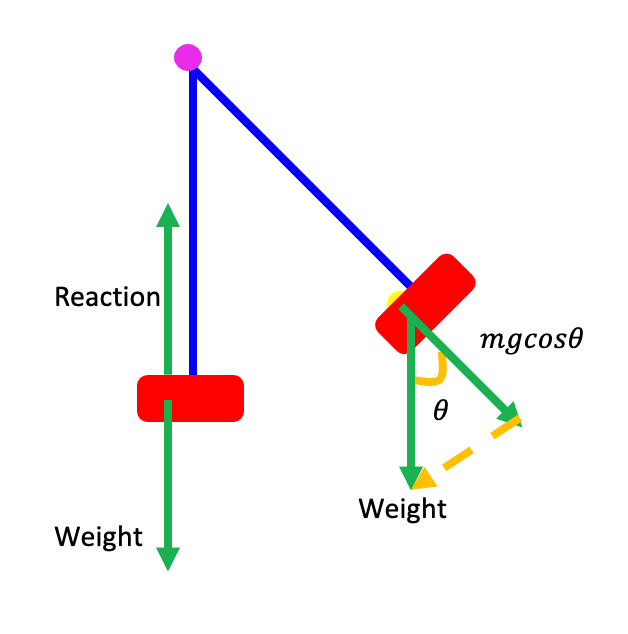
Rotor/Gravitron
- The frictional force of the wall must be equal to the weight of the rider, for the rider to stay in vertical equilibrium. The reaction of the wall on the rider provides the centripetal force.
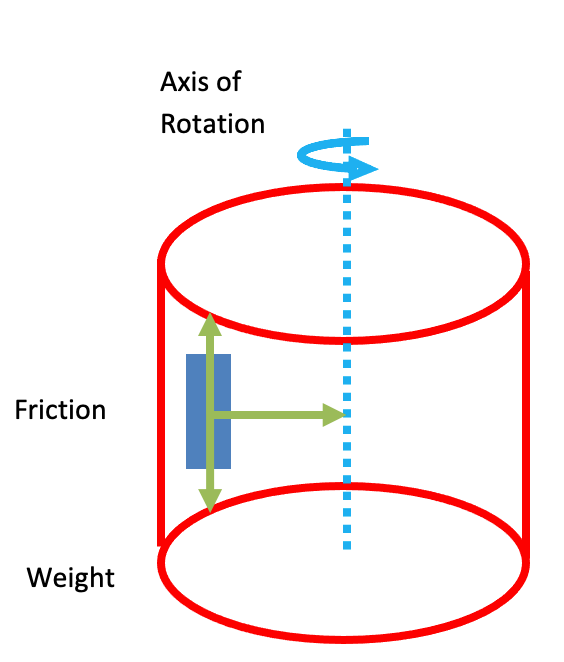
Big Wheel
- Although they rotate slowly, a centripetal force is still required. Throughout the ride, the centripetal force will be the same value, however the forces that combine to total this are constantly changing. There is always a net force towards the centre of the circle, provided by weight (top), reaction (bottom), or friction from the back of the seat (left and right), or a combination of these.
Swing Carousel (Chair-O-Planes)
- The centripetal force is made entirely of the horizontal component of tension on this ride (weight always acts vertically). The vertical component of tension then acts in the opposite direction the weight and will be equal.
- Vertical equilibrium will be established, horizontal equilibrium won’t be established, and this unbalance causes the usual centripetal acceleration
Spinning Faster and Faster:
Moment of Inertia
- Resistance to change in angular motion is measure by the moment of inertia about a chosen axis for the object. A ratio of torque-to-acceleration. Measured in units of kgm^2
- Example
- If a disc and hoop of identical mass and radii roll down the same incline the hoop will take longer to reach the bottom
- Reason is because more of the hoop’s mass is distributed further from the centre of its axis rotation
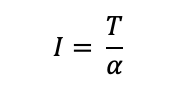
Torque
Torque (moment of the force) is the product of the force and the perpendicular distance between the line of action of the force and the axis, measured in Nm.
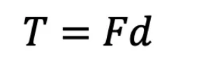
Momentum
Table to show the similarities between linear and angular momentum
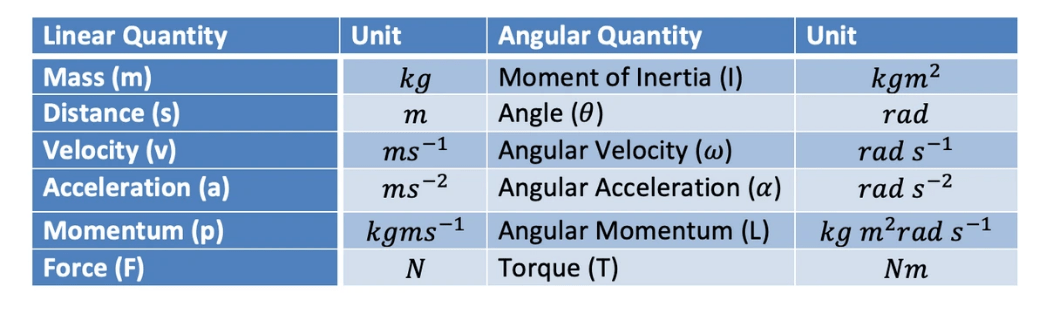
Using this possible to easily write down equations for angular acceleration by replacing linear quantities with angular quantities
- F=ma becomes T=Iα
- p=mv becomes L-Iω
- W=Fs becomes W=Tθ
- Also works with the equations of motion (SUVAT)
Rotational Kinetic Energy
There are two types of kinetic energy need to be considered when looking at something in circular motion: translational and rotational. Translational kinetic energy is the linear energy need to move an object from point A to B. Rotational energy is the energy used to make an object to rotate. When a circular object rolls down a slope, both these types of kinetic energy are involved, therefore the loss of GPE is turned into both types of kinetic energy.
- Translation (normal) kinetic energy
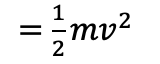
- Rotational (angular) kinetic energy
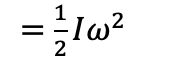
Meaning the total kinetic energy of a rolling object is given by
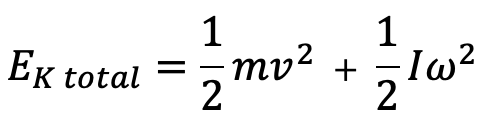
Conservation of Angular Momentum
The concept of conservation of angular momentum is very important in amusement park rides. In a similar way to linear momentum, the system is required to be isolated with no external torque acting. The total angular momentum of the system will remain constant.
The moment of inertia is deliberately changed in many rides, and is achieved through changing the distribution of mass. It results in acceleration (α= T/I)
- Example
- Child on a freely rotating roundabout moves closer to the centre of the roundabout, therefore the radius of the circle is reduced
- This would then violate the conservation of the angular momentum if the roundabout would continue to rotate at the same speed as the moment of inertia has been reduced
- In order for the angular momentum to remain the same with the moment of inertia reducing, an increase in angular velocity is needed
In amusement park rides, altering the moment of inertia can be helpful
- The Waltzer
- Rotating buckets are mounted on a track attached to an oscillating segmented floor
- Motion is complex- a combination of vertical SHM, horizontal circular motion and oscillation of the bucket
- Rider can alter the angular speed through changing the moment of inertia
- Moving away from the centre of rotation
- Moment of inertia decreases àAngular speed decreases
- Moving in towards the centre of rotation
- Moment of inertia increases àAngular speed increases
- Moving away from the centre of rotation
- Swinging ride
- Two cars swing symmetrically in opposite directions
- Cars will have equal and opposite angular momentum, meaning they will cancel out the torques on the supporting axle
And we're all done for today!

Drafted by Kin (Physics)

