·
Quadratic Equations
Quadratics can be solved by:
- factorisation
- using the formula
- completing the square
- graphically (using x intercept/s - only when line touches x axis)
Solving (x-5)(x-5) = 0
- One of the brackets has to = 0 in order to multiply to get 0
- so (x-5) = 0
- so x = 5
- X is inverse of what is in the bracket
- Always show that brackets = 0 as it is an equation not an expression.
Formula
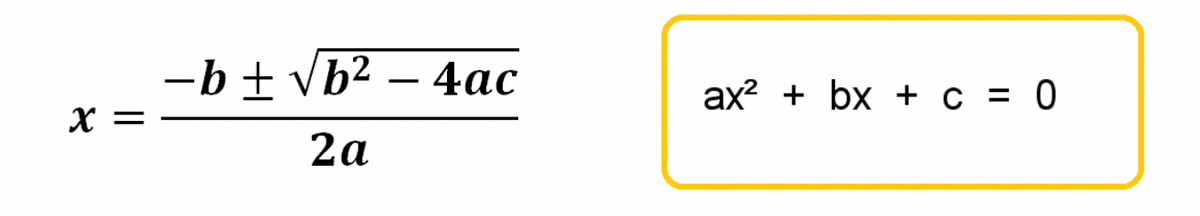
Completing the square
- a/co-efficient of x² must be 1
- x² + 5x + 4 = 0
- Divide b by 2
- Put x² + b/2x into bracket
- Expand to find (b/2)²
- Repeat step 2, but -(b/2)² and +c
- e.g. (x - 2)² - 5 = 0
- (x - 2)² = 5
- (x - 2) = √5
- x = √5 + 2 or x = - √5 + 2
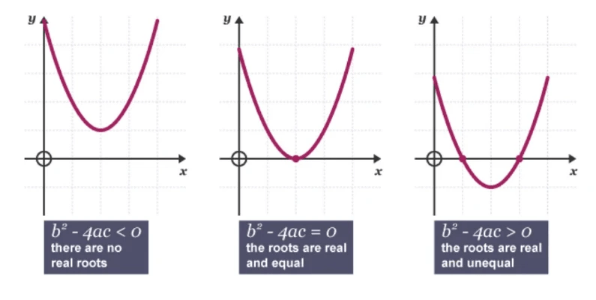
The Discriminant
- Positive = b² - 4ac > o (2 solutions)
- Neutral = b² - 4ac = o (1 solution)
- Negative = b² - 4ac < o (no solution)
- Math error = no solution a.k.a on graph the parabola does not cut the x axis.
When it comes to IGCSE/GCSE Maths, do you remember how to work out the turning point?
The Turning Point
- Vertex of the parabola - halfway between the roots.
- If the turning point is the highest point = maximum point.
- If the turning point is the lowest point = minimum point.
- By completing the square of a quadratic,
- y = a(x+p)² + q
- a > 0 — minimum point (below x axis)
- a < 0 — maximum point (above x axis)
- Turning point = (p,q)
- a(x+p)² + q
- p = inverse of p (-p)
- q = q
Completing the square when a >1
- y = 2x² + 12x + 1
- Divide everything by co-efficient of x to put it outside the bracket.
- Complete the square within the bracket.
- Expand (by co-efficient) to eliminate outside bracket.
- Then locate p and x.
Quadratic Inequalities
- Solve the inequality as an equation.
- Check if graph is min/max point (co-efficient of x > or < 0).
x² - b > 0 — x > highest, x < lowest
x² - b < 0 — lowest < x < highest
That's the end of the topic!

Drafted by Bonnie (Mathematics)

