In this topic of IBDP Mathematics, we will be learning about venn diagrams, and how we can solve problems using venn diagrams. This topic is in the core part of the HL and SL syllabus, so is required for all IB Maths student.
Venn Diagrams
In IBDP Mathematics, we have discussed the idea of sets (if you need a refresher on sets, click here). A good way to visualise sets is to use venn diagrams.
- Venn diagrams consists of a universal set U represented by a rectangle, and subsets within it which are represented by circles.
- Each circle within the rectangle represents one subset within the universal set. The number of circles in the venn diagram should correspond with the number of subests you have within the universal set.
- It is important to remember to draw the universal set each time. You may be used to venn diagrams consisting just of circles, but in IBDP Mathematics, it is not a venn diagram if the universal set is not represented.
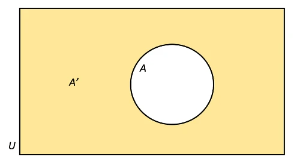
- The venn diagram above shows the set A (represented by the circle) within the universal set U (represented by the rectangle).
- The complement of A is represented by the shaded region outside the circle.
If we were to use venn diagrams to represent subsets, it would look like this.
- Say set B is a subset of set A. This means that every element of set B is also an element of set A.
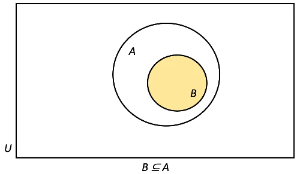
- The circle representing set B is placed within the circle representing set A - this is how we can represent subsets using venn diagrams.
Sometimes, sets may have some elements in common, but they are not subsets of each other - these are known as intersecting sets. In these cases, we can draw the circles overlapping each other.
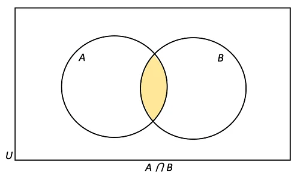
- Say set A and set B are intersecting sets. The venn diagram below represents set A and B.
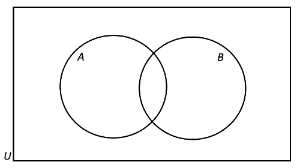
- The intersection of set A and B (A ⋂ B) is represented by the parts of the circles which overlap.
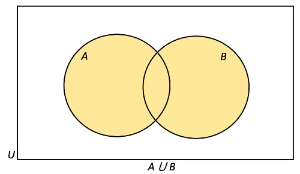
- The union of set A and B (A ⋃ B) consists of all elements in A or B or both. It is represented by all the regions included in both circles.
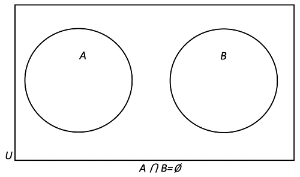
Sets which are disjointed or mutually exclusive do not overlap. They can be represented by non-overlapping circles.
In order to familiarise yourself with venn diagrams and set notation (e.g. intersections, unions, complements), you can click here and work through the different levels.
- Tip: when working through the more complex venn diagrams, it would be useful to identify the part of each set required (i.e. which regions of set A and which regions of set B are included) separately, before combining them into one venn diagram.
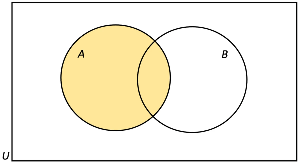
- For example: Say we had to shade the regions A ⋃ B'.
- We would first colour the regions required from set A - we need to whole of set A.
- We would then consider the regions required from set B - we need the complement of B, thus all the regions that are not included in the circle B.
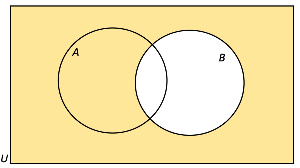
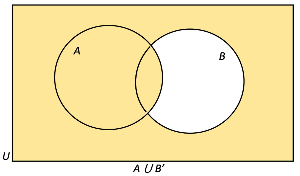
- Now, because the question requires us to shade the union of these two regions, thus we simply combine the two separate venn diagrams into one, and shade all of the regions that are shaded in both venn diagrams.
In IBDP Mathematics, sometimes you will have to illustrate the given sets using venn diagrams. Below is an worked example question showing how we can visualise sets using venn diagrams.
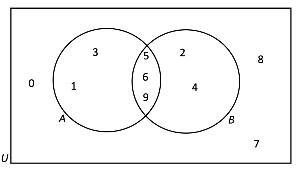
- Say U = {0,1,2,3,4,5,6,7,8,9}, A = {1,3,5,6,9} and B = {2,4,5,6,9}. Illustrate these sets on a venn diagram.
- First, we can immediately identify the elements within each set and write them into the venn diagram.
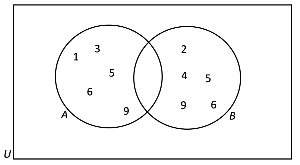
- Next, we can see that the sets A and B have some elements in common: A ⋂ B = {5,6,9}. We can write these numbers into region where the circles overlap to indicate that they are included in both sets.
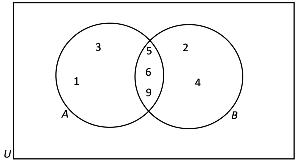
- Finally, there are still some numbers in the universal set that are not in set A or B - these need to be written within the rectangle, but outside of the two circles.
In IBDP Mathematics, sometimes we are more interested in the number of elements within each set rather than the actual elements within each set. To represent the number of elements in the set (rather than the elements themselves), we can write the number in brackets within each area.
- For example, in the venn diagram below, we can see that there are 5 elements in set A but not B, 3 elements in set B but not A, elements in A ⋂ B, and 2 elements that aren't in either set A or B, but is in the universal set.
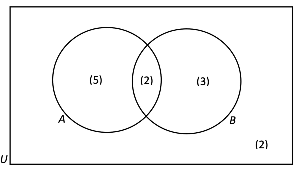
- From this, we can deduce the number of elements in set A and B, and the number of elements in the universal set, the number of elements in A ⋃ B and more.
- n(A) = 5+2 = 7
- n(B) = 3+2 = 5
- n(U) = 5+2+3+2 = 12
- n(A ⋃ B) = 5+2+3 = 10
Problem Solving using Venn Diagrams
In IBDP Mathematics, we can use venn diagrams to visualise information given, and then use the information to answer questions. With these questions, we are typically more interested in the number of elements in each set rather than the actual elements.
Here is a worked example of how we might use venn diagrams to help answer questions:
Sam has 14 hamsters as pets. 5 of them have long hair, and 8 are brown. 2 have both long hair and are brown. First, place this information on a venn diagram and then use the venn diagram to find the number of hamsters that i) do not have long hair, ii) have long hair and are not brown, and iii) are neither long haired nor brown.
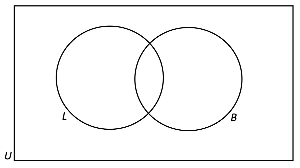
- First thing we do is to draw this information up in a venn diagram. To do this, we first have to identify the sets that exist within the universal set.
- The universal set in this question is the 14 hamsters. There are two subsets within the universal set - the set of hamsters with long hair, and the set of hamsters that are brown. We can name these sets as L (for long hair hamsters) and B (for brown hamsters). Thus, the basic structure of our venn diagram would look like this:
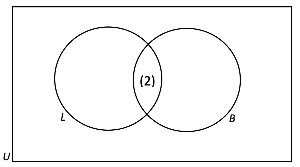
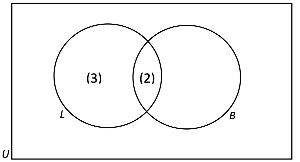
- Now, we can start filling in the information. One tip when filling in information in venn diagrams, we always work from the center out. In other words, we write out the information in the intersection of all the sets first, before moving outwards.
- Based on the information given in the question, there are 2 hamsters that are long hair and brown - this would mean that there are 2 elements in the intersection of L and B. Thus, we can write that down in the intersection of the circles.
- The question also tells us that 5 of the hamsters have long hair. This means that n(L) = 5. However, we cannot just write 5 in the L circle. We also need to take into consideration the 2 in the intersection. These two are also hamsters with long hair, thus are part of the 5 long haired hamsters. In the end, there are only 3 hamsters that are long haired (but not brown), so we write 3 in the L circle.
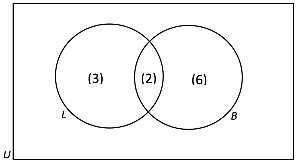
- Now, we can repeat the process with the brown hamsters. There are a total of 8 brown hamsters, thus n(B) = 8. However, when writing it in the B circle, we need to take into consideration the 2 hamsters that are brown and long haired, thus there are only 6 hamsters that are brown (but not long haired). We write 6 in the B circle.
- Lastly, we need to consider the hamsters that aren't in this set. We can do this by finding the number of elements in the union of sets L and B, and subtracting it from the number of elements in the universal set.
- n(L ⋃ B) = 3+2+6 = 11
- n(U) = 14
- Therefore, the number of elements that aren't in either L or B is 14 -11 = 3 .
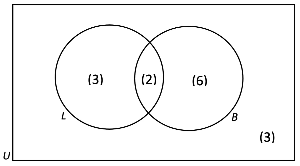
- This is the complete venn diagram. Now we can use this venn diagram to answer the questions.
- The number of hamsters that don't have long hair: This is equivalent to the number of elements that aren't in set L (i.e. n(L')). This includes the region that aren't included in L.
- n(L') = 6+3 = 9.
- The number of hamsters that have long hair and aren't brown: This is equivalent to to the number of elements that are in L, but aren't included in L ⋂ B (i.e. n(L ⋂ B')).
- n(L ⋂ B') = 3
- The number of hamsters that are neither long haired or brown: This is equivalent to the number of elements that are not included in either set L or B, but are in the universal set (i.e. n((L ⋃ B)')).
- n((L ⋃ B)') = 3
If you get confused about which regions to include when answering questions, simply colour in the regions that are included, and take the sum of the numbers within each included region.
This is the end of this topic.