In this topic of IBDP Mathematics, we will be learning about different special number sets, as well as the notation used to write intervals. This topic is in the core part of the HL and SL syllabus, so is required for all IB Maths students.
Special Number Sets
In IBDP Mathematics, there are several special number sets you need to know. These special number sets are infinite sets, so they contain an infinite number of elements.
The first special set you need to know is the natural numbers.
- The set of natural numbers consist of all positive whole numbers - these are the numbers you count with.
- Natural numbers are denoted by this symbol: ℕ
- Using set notation, the set of natural numbers can be defined as ℕ = {0,1,2,3,4,5,6,7,8,9,10,11,...}

Another set of numbers you need to know is integers.
- The set of integers consist of whole numbers, both positive and negative.
- Integers can be denoted by this symbol: ℤ
- Using set notation, the set of integers can be defined as ℤ = {0,±1,±2,±3,±4,±5,±6..}

We can also write the set of positive integers.
- This set, as indicated by its name, consist of only the positive integers.
- The set of positive integers can be denoted by this symbol: ℤ+
- Using set notation, the set of positive integers can be defined as ℤ+ = {1,2,3,4,5,6...}
- As you may have already realised, we can say that ℤ+ is a subset of ℤ, as all the elements in ℤ+ are also elements of ℤ.

Another set of numbers is rational numbers.
- This set consist of numbers that can be written in the form p/q, where p and q are integers and q does not equal 0.
- An example of a rational number would be 1/2, or -6/4. These are considered rational numbers, as they can be written as a fraction, with the numerator and denominator as integers.
- The set of rational numbers can be denoted by this symbol: ℚ
- All decimal numbers that terminate (i.e. have a finite number of decimal places) or recur (i.e. decimal numbers that repeat infintely) are rational numbers.
- e.g. 0.333... is a rational number, even though it has infinite decimal places, as it can be written as 1/3.
- It is important to note that all the number sets above (i.e. integers and natural numbers) are a subset of rational numbers. All whole numbers can be written in rational form, thus integers and natural numbers are a subset of rational numbers.
The complement of rational numbers is irrational numbers.
- Irrational numbers are the numbers that cannot be written in rational form, but are still can be placed on the number line.
- Most (if not all) surds are irrational numbers. An example of irrational numbers would be √2 or pi.
- The set of irrational numbers can be denoted by this symbol: ℚ'
- Given that irrational numbers are numbers that cannot be written in rational form, we can say that irrational numbers are the complement of rational numbers, with the universal set being numbers that can be placed on the number line.
Finally, we have the set of real numbers.
- Real numbers are the set of all numbers which can be placed on the number line - this includes all rational and irrational numbers.
- The set of real numbers can be denoted by this symbol: ℝ
- Note that since real numbers includes all rational and irrational numbers, we can say that ℝ = ℚ ⋃ ℚ'.
- We can consider real numbers to be the universal set, with rational and irrational numbers being complements of each other within this universal set.
- All of the numbers sets listed above are subsets of real numbers - all of the number sets consist of elements that can be placed on the number line.
- Since numbers such as √-3 and 1/0 cannot be written on the number line, they are not real numbers.

Interval Notation
In IBDP Mathematics, there are often times where you will need to describe a set of consecutive numbers within the special number set (e.g. when defining the domain of a function). There are several ways to do this.
Say we are asked to describe the set of integers in between -4 and 3. We can do this by...
- Simply using set notation and listing the set {-3,-2,-1,0,1,2}
- We can also illustrate the set as points on the number line.
- Alternatively, we can also use interval notation.
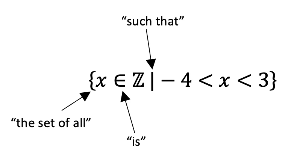
- This can be read as "the set of all integers x is such that x lies between -4 and 3."
- The curly brackets indicate that this is a set, whilst the first part of the interval tells us that x is an integer. The last part of the interval notation tells us what the values of x are.
For example, if we want to use interval notation to represent all the real numbers between -2 and 4 (including -2 and excluding 4), we can write {x ∈ ℝ| -2 ≤ x < 4}.
- This can be read as "the set of all real x such that x is greater than or equal to -2, and less than 4."
- More commonly, if we are referring to the set of real numbers, then we don't need to specify that x is a real number.
- i.e. we can also write this interval as {x | -2 ≤ x < 4} - in this case, we assume that x ∈ℝ.
This interval can then be represented on the number line:

- In this number line, the filled circle indicates that -2 is included in the interval, whereas the open circle indicates that 4 is excluded from the interval.
In IBDP Mathematics, we can also use bracket notation to concisely write intervals. It is important to note that when using bracket notations, it is assumed that we are referring to the set of real numbers.
- [a,b] represents the closed interval {x | a ≤ x ≤ b}
- ]a,b] represents the interval {x | a < x ≤ b}
- [a,b[ represents the interval {x | a ≤ x < b}
- ]a,b[ represents the open interval {x | a < x < b}
All of these intervals have an endpoint. But some intervals can extend to infinity - for example {x | x ≥ 4}. For this interval, we can write [4,∞[. More generally,
- For intervals {x | x ≥ a}, we write [a,∞[.
- For intervals {x | x ≤ b}, we write ]-∞, b]
- It is important to note that when using bracket notation to write out intervals that extend to infinity, the bracket closest to the infinity sign is facing away.
When writing bracket notation, it is important to remember that if the bracket is facing inwards (towards the interval values), this means that the value is included in the interval. If the bracket is facing outwards (away from the interval values), this means that the value is excluded from the interval.
This is the end of this topic.


