IBDP Mathematics Long Question Analysis Topic: Mathematics - Circumscribed Triangle
Exam Question:
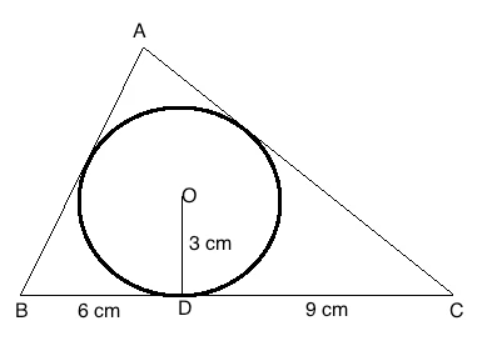
In Figure 5, a △ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively of lengths 6 cm and 9 cm. If the area of △ABC is 54 cm2, then find the lengths of sides AB and AC.
Answer:
For IBDP Mathematics, you should know:
First, let's establish some "givens". We know that:
1. OD = 3 cm
2. BD = BE = 6 cm (equal tangents)
3. DC = CF = 9 cm (equal tangents)
4. Area of triangle ABC = 54 cm2
Now, let's start calculating:
1. Area of triangle OBC = 1 / 2 x 15 x 3 = 45 / 2 cm2
2. Area of triangle OAC = 1 / 2 x (x + 9) x 3 = 3(x + 9) / 2 cm2
3. Area of triangle OAB = 1 / 2 x (x + 6) x 3 = 3(x + 6) / 2 cm2
54 = 3 / 2 [(x + 9) + (x + 6) + 15]
> 54 = 3 / 2 x (2x + 30)
> 54 = 3(x + 15)
> 17 = x + 15
> x = 2
Then, we can calculate the length of the sides as:
x + 9 = 2 + 9 = 11; x + 6 = 2 + 6 = 8
Altogether, the sides of triangle ABC are 11, 8 and 15 units.
Below is the completed diagram for your reference.

Work hard for your IBDP Mathematics examination!
End of analysis. Great!


