GCSE Mathematics Question Analysis Topic: Mathematics - Long Question
Exam Question:
In a right triangle ABC, right-angled at B, BC = 12cm and AB = 5cm. What is the radius of the circle inscribed in the triangle (in cm)?
Answer:
For GCSE Mathematics, you should know:
First, let's check out our given information.
AB = 5cm and BC = 12cm.
By using Pythagoras' theorem,
AC2 = AB2 + AC2
= 52 + 122
= 25 + 144
= 169
Therefore, AC = 13 units.
Next, we have to remember a crucial point regarding tangents:
"Two tangents drawn to a circle from the same point exterior of the circle are of equal lengths."
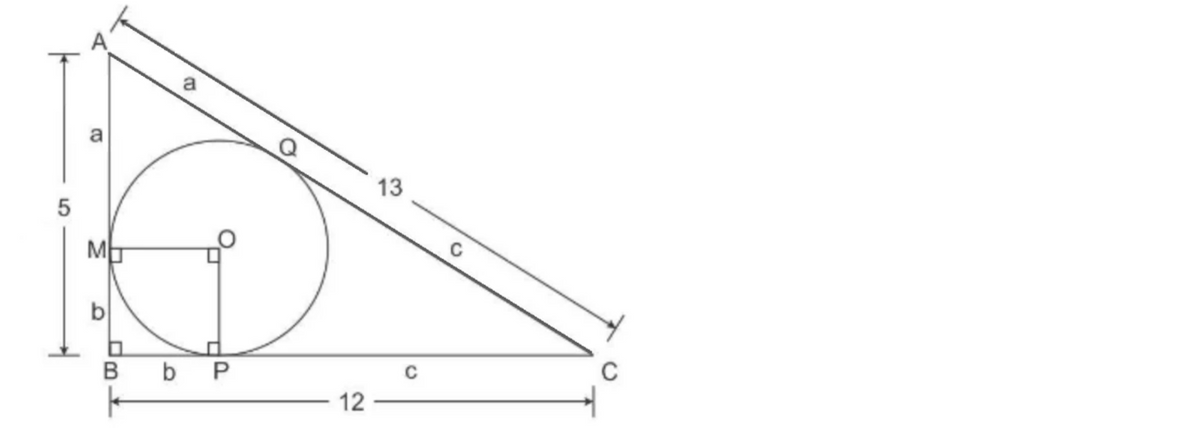
Looking at the graph, we can see:
AM = AQ = a
Similarly, MB = BP = b and PC = CQ = c.
We now know that:
AB = a + b = 5
BC = b + c = 12
AC = a + c = 13
By using the method of solving simulatenous equations, we get:
a = 3, b = 2 and c = 10.
Another rule to remember is that tangents are always perpendicular to the radius.
Thus, OMBP is found to be a square, with sides b.
From this, we can see that the radius' length in the right-angled triangle is 2cm.
The following sketch is for your reference.
Work hard for your GCSE Mathematics examination!
End of analysis. Great!


