·
Differentiation
- This is used to find the gradient of a curve at different points.
- It also helps us find the equation of a tangent or a normal to a curve, stationary points on a curve, minimum and maximum points and tells us whether a function is increasing or decreasing.
- Times by the power, then take one away from the power.
- E.g. x5 becomes 5x4
- E.g. 3x becomes 3
- Rule: x becomes 1
- Rule: 6 becomes 0
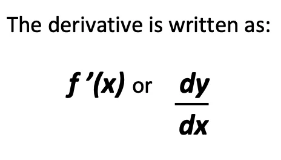
- If they give you the gradient and the equation, simply find x by putting it equal to the derivative and then sub in your x value into the original equation.
- Always expand and simplify before differentiating and cancel afterwards.
Rates of change
- Differentiate it as you would a normal equation/function.
- They will also give you a value to sub into your derivative (this is like the ‘x’ value in an equation).
- The key is to treat it like an equation, but do not forget the units (may need to figure out the units according to the variables they have given you e.g. cm per second or cm-1).
Equation of a tangent to the curve
- The tangent to the curve touches the curve.
- The tangent is a straight line (therefore, all the straight line rules and equations apply to it).
- The gradient of the point where the curve and tangent touch is the same.
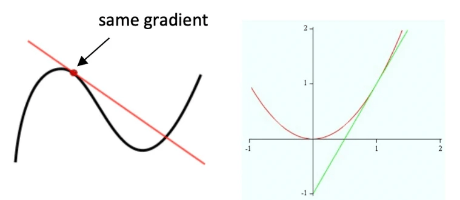
To find the equation of a tangent when they give you the equation of the curve and the x coordinate:
- Differentiate equation of the curve (so you can find dy/dx or the gradient).
- Sub in your x value, to find your gradient.
- Go back to your original equation, sub in your x value, then find y.
- Use your x value and y value (your coordinates) to find the equation of the tangent using y - y1 = m(x - x1).
Equation of a normal to the curve
- The normal to curve is always at a right angle to the tangent.
- This means that it is perpendicular to the tangent.
- This means that the product of the gradients is -1.
m1 x m2 = -1
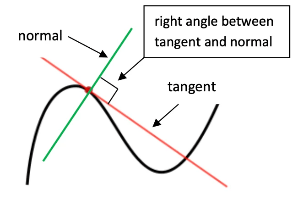
To find the equation of a normal when you are given the equation of a curve and an x coordinate:
- You find the gradient of the tangent first.
- Then substitute the tangent’s gradient (m1) into the equation above, to find the normal’s gradient.
- Then find the y value by subbing x into the original equation of the curve.
- Then you can use m2 and your coordinates to find the equation of the normal.
Stationary points
- A stationary point is a point on a curve where the gradient is 0.
- This means that dy/dx or f’(x) is also going to be 0.
- If you’re asked to find a stationary point on a curve, simply:
- Differentiate
- Put the derivative equal to 0
- Solve it by either:
- Rearranging to get the cube root if it’s a cubic graph
- Factorising to find two values of x if it’s a quadratic graph
- Rearranging and solving if it’s a linear graph - Sub the x value back into the original equation and find your y value, then you have your coordinates.
When it comes to IGCSE/GCSE Maths, do you remember how to find maximum and minimum points?
Minimum and Maximum points
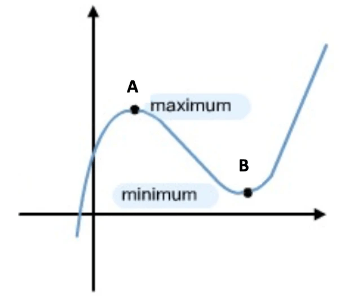
- A stationary point is either a minimum or a maximum point.
- E.g. A is a maximum point because at A, dy/dx = 0.
- When the curve goes down, the gradient will decrease.
- This means that dy/dx < 0.
- E.g. B is a minimum point because at B, dy/dx = 0.
- When the curve goes up the gradient will increase.
- This means that dy/dx > 0.
- For minimum and maximum points, you need to differentiate twice i.e find f ’’(x) and then sub in your x coordinate into your second derivative.
Increasing and decreasing functions
- If the gradient of a function is positive then it is increasing.
- If the gradient of a function is negative then it is decreasing.
- When you multiply or divide by a negative number, you have to reverse the inequality.
- E.g. x² > 0 → -3x² < 0
That's the end of the topic!

Drafted by Bonnie (Mathematics)

